D(データ)フェーズで整理したデータをもとに分析を行い、問題解決につながる要因を発見します。
このフェーズでは、理解を促すための可視化が特に重要です。数値の集まりであるデータも、表やグラフで可視化することで、特徴や傾向が見えるようになり、効率的な分析が行えます。
ここから本文です。
ゼミナール編(1) 〜データ利活用の進め方
1時限目 データ利活用の進め方
〜 実例で見るPPDACサイクル 〜

A(analysis、分析)データに基づく分析
データを分析する際の4つの視点
分析というと、専門性が高そうなイメージがありますね。もちろん、専門性は高いのですが、分析の本質は、何か新しいもの、未知のものに出会ったときに人間が行う認知の過程と大きく変わらないともいえます。4つの視点を追っていきましょう。
1 全体を見渡す
おおよそをつかみます。全体の傾向や分布を見ます。何を表しているか? 最大値は? 最小値は? 平均値は? 中央値は? 最頻値は? 散らばりは?
2 分ける・比べる
年齢、地域、男女、その他考えられるグループや条件で分類し、比較します。分けてみると1で見た全体像とちがったものが見えてくる場合もあります。「分ける・比べる」はデータ分析の呪文のようなもの。どのように分け、何と比べるかでデータの裏に隠れていたものが見えてくる可能性もあります。アンケートなどでのクロス集計もその一つです。
3 変化や関係を探る
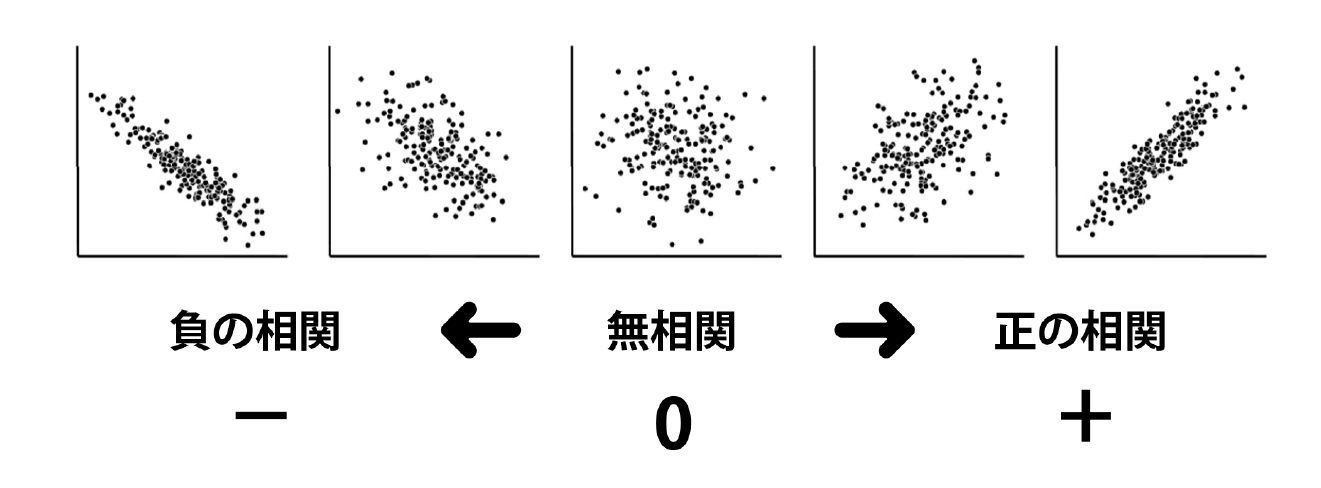
変化の代表指標は「時間」です。時系列変化を探りましょう。また、変化の「大きさ」も大事な注目ポイントです。成長率、増減率などで表現されますが、一定の割合で増加(減少)していたものにブレが生じたのはなぜか? そこには必ず理由があるはずです。
関係とは、2つ以上の指標の関連性を指します。代表的なものに相関関係があります。ここで気をつけたいのは、相関関係と因果関係(原因と結果)は全くちがうものだということです。相関があると判定されても、それは2つの指標の動きを示したものであり、因果関係を示すには他の分析が必要です。
散布図と相関係数の関係
4 予測する
1〜3の過程を踏むと、日常の物事に関していえば、人は何となく予測、推測ができるようになりますね。往々にしてはずれたりすることもありますが‥。一方、データ分析の分野では、適切なデータと統計手法を用いることで「予測モデル」や「因果説明モデル」を作成することができます。回帰分析がその例です。複数の変数(要因や事象など)の関係を数式化します。その確からしさも数値化されます。予測モデルもしくは因果説明モデルの作成まで到達することがデータ分析の醍醐味ともいえるかもしれません。
専門家との外部連携
高度な分析を行うには、行政の現場だけでは手に負えない場合もあるでしょう。
データ分析の支援体制として、外部組織(大学やシンクタンク、独立行政法人、民間コンサルタント等)と連携スキームをあらかじめ立てておくことが重要です。その方法も、完全委託、人材採用、人材育成、作業支援など幅がありますので、方向性を見定め、実状にあった方法を選択するようにしましょう。
支援体制の構築とともに、職員のデータリテラシー向上のためにモチベーションや自己研鑽を奨励することは重要です。日頃から統計データに慣れ親しみ、グラフや表を見て考える習慣を身につけましょう。「考える」といっても難しいことではありません。発見をする、疑問に感じる、視点を変える、他人に意見を聴くなど、普段他の案件でやっていることと変わりはありません。
 滋賀県の実践例
滋賀県の実践例
滋賀県事例における、ここまでのPPDACサイクルを振り返ってみましょう。
- P(問題)‥M字カーブの底上げのための要因は何か?
- P(計画)‥考えられる要因をあげ、ロジックツリーで整理
- D(データ)‥整理された要因に関する20項目の統計データを収集・整理
A(分析)ではDで収集した統計データに対し、図のような流れで要因を絞り込み、要因分析を行いました。
分析の流れ
| 目的 | 分析手法 | 分析結果 | |
|---|---|---|---|
 |
30歳代有配偶女性労働力率と各要因との関係性を定量的に把握する | 相関分析47都道府県データを利用 | 13要因について、散布図による視覚化と相関係数による数値化が完了 |
 |
|||
 |
13要因の関係を定量的に把握し、要因を絞り込む | 主成分分析13要因の相関係数を利用 | 30歳代有配偶女性労働力率に大きく関与すると考えられる7要因が判明 |
 |
|||
 |
6要因の影響度を比較する | 重回帰分析7要因のうち相関が極度に強い要因を排除して6要因で実施(多重共線性の回避) | 統計的に有意と判定される重回帰モデルが作成され、要因分析の完了 |
なお、滋賀県の実践例では、滋賀大学と連携しつつも、EBPM推進の観点から政策立案に関与する滋賀県の担当者が、自ら分析を実行でき、分析結果の解釈ができることを考慮して分析を進めたということです。
 相関分析 〜 分けて比べて、2つの関係を探る
相関分析 〜 分けて比べて、2つの関係を探る
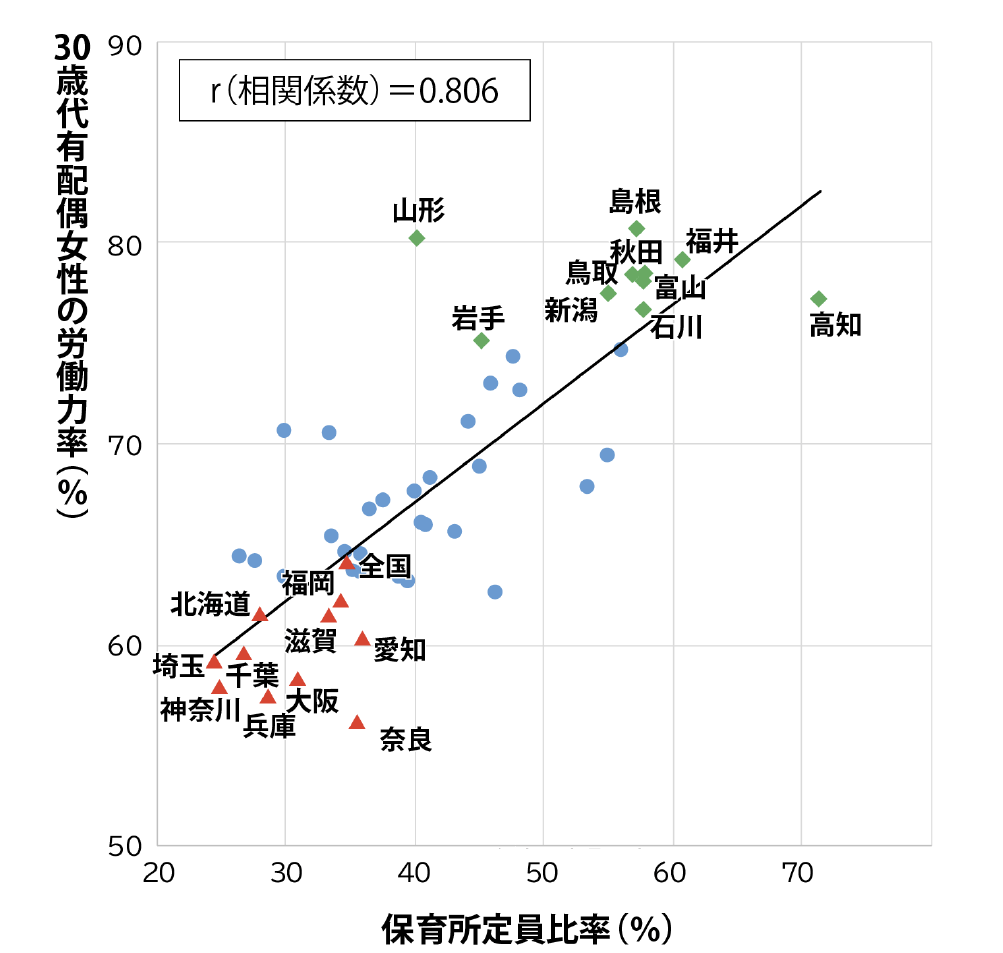
収集されたデータを吟味し、分析に足るデータであると判断された13項目(*)について、「30歳代有配偶女性の労働力率」との相関関係を調べました。
*ロジックツリーにある「介護」「健康」は、収集されたデータを調べたところ、30代女性の離職理由や非就業理由として割合が非常に小さかったため分析から除外されました。
 主成分分析 〜 3つ以上の関係を定量化
主成分分析 〜 3つ以上の関係を定量化
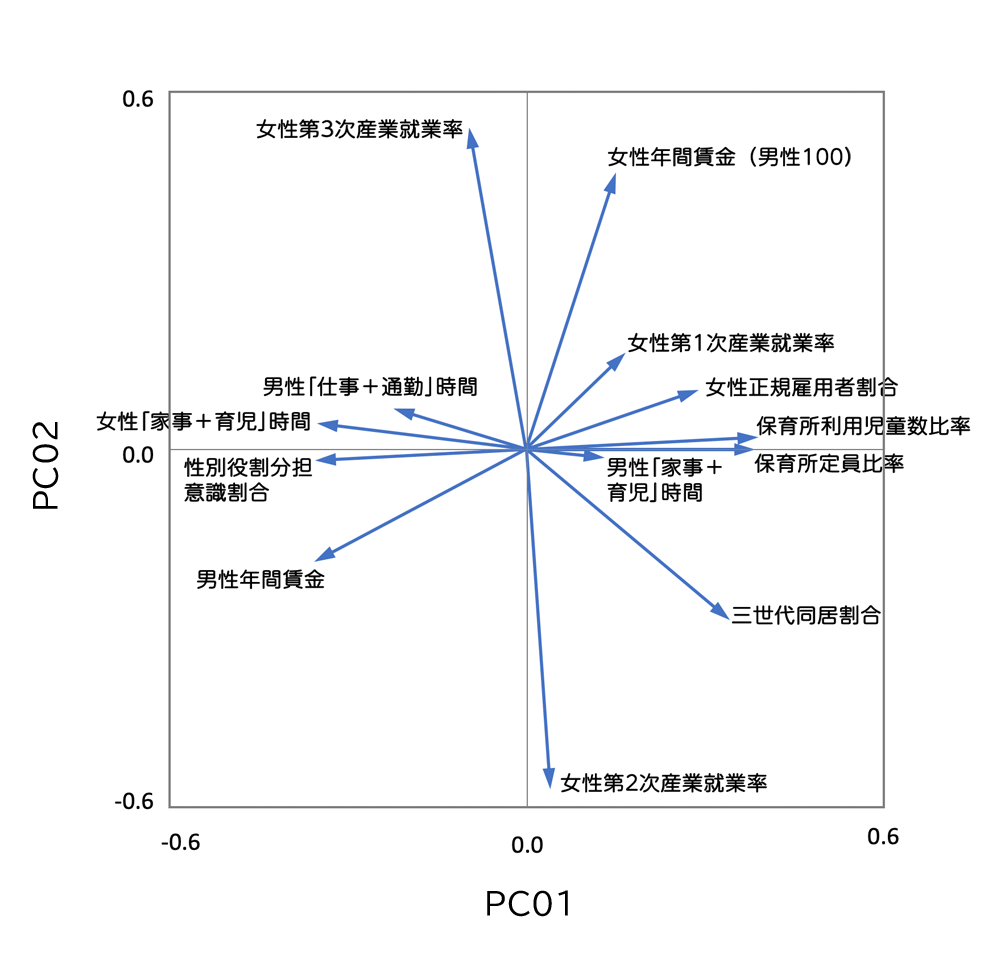
主成分分析により、13要因の全体的な関係を定量的に把握し、30歳代有配偶女性の労働力率と関係が深い要因を6〜7に絞ることができました。
 重回帰分析 〜 予測モデルもしくは因果説明モデルの利用
重回帰分析 〜 予測モデルもしくは因果説明モデルの利用
回帰分析とは、結果となる数値(目的変数)と要因となる数値(説明変数)の関係性を数式モデルで表す手法です。説明変数が1つの場合は単回帰分析、2つ以上の場合は重回帰分析と呼ばれます。
数式を使って、今回の例を表してみると以下のようになります。
α1〜α6及びb(切片)の値を算出することが今回の目標です。α1〜α6は、正の値(プラス)になることも負の値(マイナス)になることもあります。
上記の式は、6つの要因に係数(α1〜α6)をかけて足し合わせると、結果が推測されることを表します。逆に言うと、係数の正負と絶対値の大きさにより、より高い結果を出すためには、どの要因の数値を上げればよいか、下げればよいかという効率的な判断もできうるということにもなります。
え? それならば13要因のデータを集めたのだから、全て使えばよかったのでは? 予測の精度が上がるのでは?と思う方もいらっしゃるかもしれません。重回帰分析では、説明変数が多すぎるとモデルの検証が難しくなることと同時に、説明変数間に強い相関があるものが含まれているときは、係数が正しく計算できなくなる(多重共線性)という特徴があります。「1相関分析」「2主成分分析」の過程を経た理由の1つはここにあります。
今回の事例でいうと、主成分分析の結果で最後に残った7要因のうち、「保育所定員比率」と「保育所利用児童数比率」は相関係数0.961と高いため、「保育所定員比率」が選択され、6要因での重回帰分析が行いました。
この「多重共線性」は言葉としては難しいですが、重回帰分析を行うときの重要ポイントですので、頭の片隅にちょっと置いておくとよいでしょう。
●重回帰分析の結果
重回帰分析の目的変数と説明変数を以下のように設定し、表計算ソフトの(Microsoft社Excel)のデータ分析アドインツール「回帰分析ツール」で重回帰分析を行った結果の出力は次の図の通りです。これを見ると、精度が高く、統計学的にも意味のある重回帰モデルが作成されたことがわかります。
(目的変数)30歳代有配偶女性の労働力率
(説明変数)
(1)女性正規雇用者割合(%)
(2)女性の「家事+育児」時間(分)
(3)性別役割分担意識(%)
(4)保育所定員比率(%)
(5)三世代同居の割合(%)
(6)男性の年間賃金(千円)
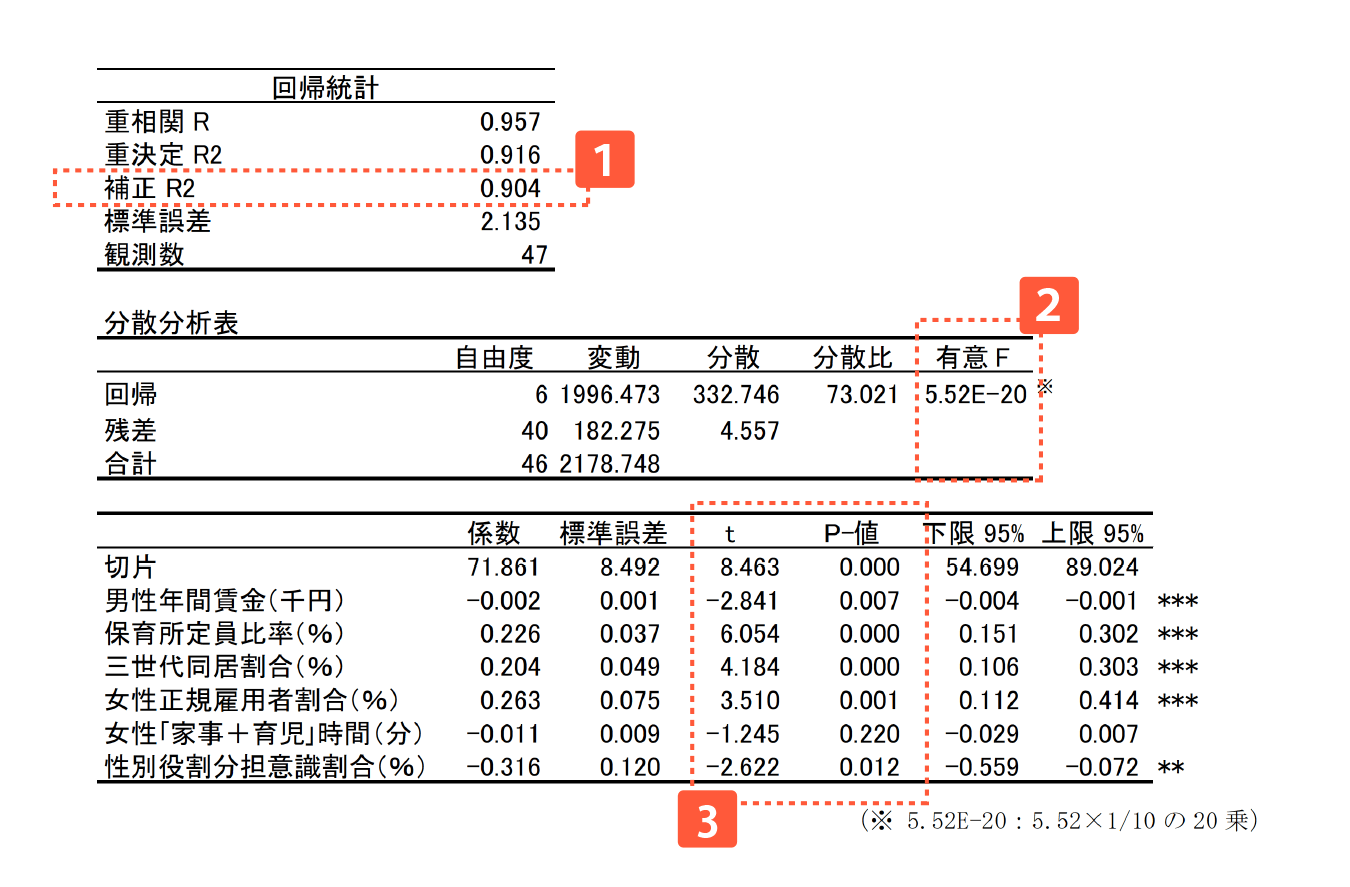

決定係数。
1に近いほど分析の精度が高く、0に近いほど分析の精度が低い。
0.904(90.4%)なのでこのモデルの説明力はかなり高い。

統計的に意味があるかどうかの指標。5.52×1/10の20乗。
つまり、0.01以下の非常に近い値となっていることから、統計的に有意である、この重回帰モデルには十分な意味があると解釈できる。

「t」はこの重回帰モデルにおける変数の影響度を表す。
「P-値」はその有意性を表し、一般には0.05よりも小さければ統計的に有意といわれる。
●重回帰モデルを利用して6要因の影響度を探る
滋賀県の女性労働力率が低い要因を分析するため、重回帰分析で得られたモデルを使い、各説明変数の全国平均との差を代入して、47都道府県との比較から検討することにしました。
以下が可視化されたグラフです。全国平均を0とし労働力率への影響度が積み上げグラフで表現されています。
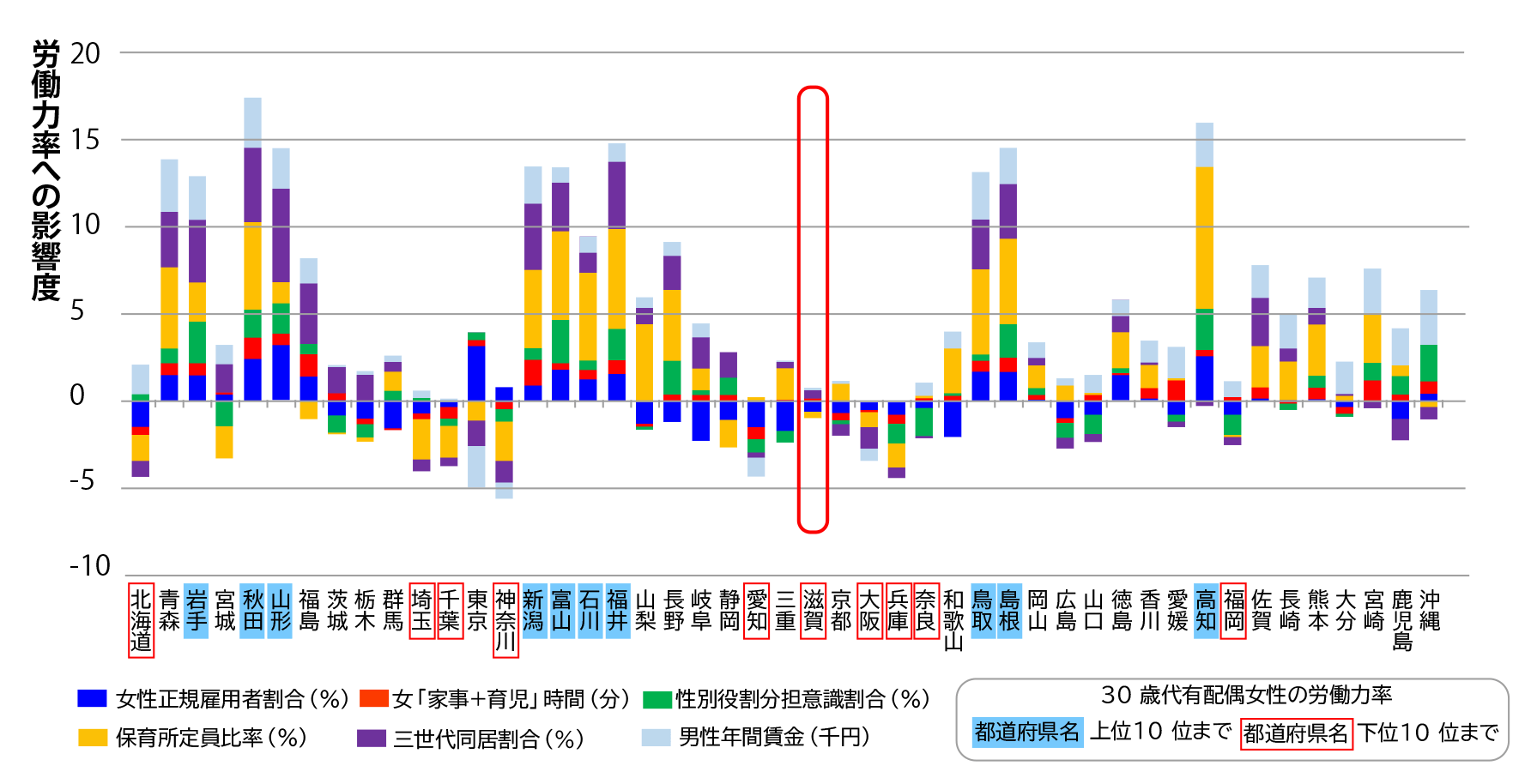
積み上げグラフの6要素は、全国平均より高いものは正、低いものは負の値となっています。このグラフから、以下のようなことが推計されます。
- 30歳代有配偶女性の労働力率の高い県の特徴は、「男性の平均年収が低い」、「三世代同居割合が高い」、「保育所定員比率が高い」が大きな割合を占めている。
- 30歳代有配偶女性の労働力率が下位の県のマイナス要因は、各道府県により異なる。
滋賀県について注目すると、滋賀県の積み上げグラフは全体的に小さいことから、全国平均との差は小さいことが読み取れます。他県と比較すると、滋賀県は最も平均的な県であり、30歳代有配偶女性の労働力率に影響を及ぼしている顕著な要因が認められない状況であると推測されました。
 ここがポイント!
ここがポイント!
- 分析の4つの視点を身につけよう。
- 予測モデルの構築は、データ分析の醍醐味。
- データ分析は、外部連携も視野に。




