標本調査では、母集団から対象となる人たちを確率的に選んで標本とします。そうなると、標本の抽出方法がまったく同じだとしても、乱数の出方によって、対象者は入れ替わりうるわけです。ここにおいて、確率的な誤差が生じます。この、標本抽出に伴って発生する誤差のことを、標本誤差と呼びます。
幸いにも、標本誤差がどのくらいの大きさになるのかは、明らかになっています。ここでは、意識調査の報告書でよく用いられる、比率(例:50%の人が内閣を支持、など)について着目し、その標本誤差について見てみましょう。
ここから本文です。
ゼミナール編(2) 〜調査実施と分析
2時限目 標本設計と調査方法
2-1 標本設計
 標本誤差の計算
標本誤差の計算
標本誤差とは
標本誤差の計算(比率の場合)
比率の標本誤差は、次の式で計算されます。
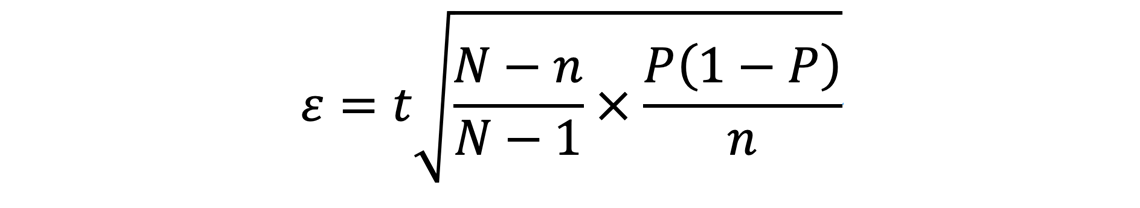
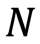 母集団の規模(人数)
母集団の規模(人数)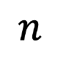 標本の規模
標本の規模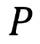 当該質問項目の比率
当該質問項目の比率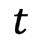 誤差の幅をあらわす係数
誤差の幅をあらわす係数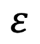 比率の標本誤差の値
比率の標本誤差の値
例えば、母集団となる20歳以上の市民が20万人いる都市で、標本として1,000人を単純無作為抽出で選んできて、調査をするとしましょう。非現実的ですが、回収率は100%だと仮定します。質問項目の比率は0.5とします。どのような値になるか事前にわからないときは、ばらつきが最大となる0.5として見積もるのがよくなされるやり方です。tの値をどうするかは統計的な基準をもとに考えますが、とりあえず2としておきます(注:正規分布の95%信頼区間の幅を概ねの目安とした)。
すると、
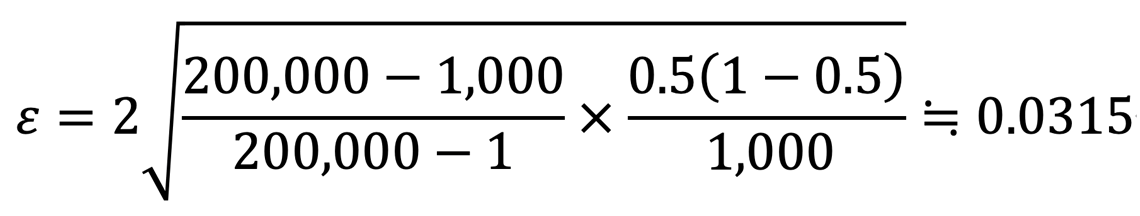
と、標本誤差εは0.0315と計算されます。つまり、この例の調査で求められる比率の値には、だいたいプラスマイナス3.2パーセンテージポイントくらいは標本誤差を見込まなければいけないということになります。
標本誤差の大きさは、調査における推定の精度ないし確からしさを意味します。もし、標本誤差をより小さくしたければ、標本規模を大きくするのがよいでしょう。
標本誤差を考慮し、調査対象人数を見積もる
この考え方、計算の仕方を応用すると、標本調査においてどれくらいの人数を調査対象とすべきか、すなわち標本規模を決める目安を見積もることもできます。上記の式を展開することで、次の式になります。
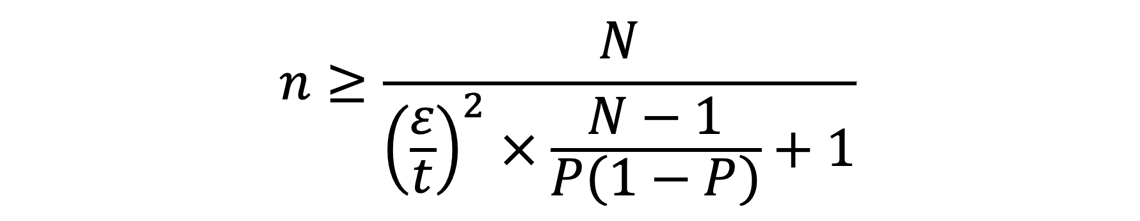
先ほどだと1,000人しか選ばなかったので標本誤差は0.0315となっていましたが、これを0.02以内にしようとしたら、いったい標本規模を何人とすればよいでしょうか。N、P、tは先ほどと同じ値にし、さらにεを0.02とすると、次のように計算されます。
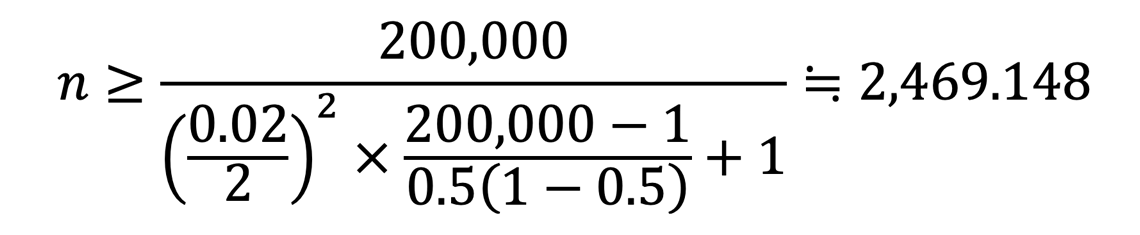
要するに、2,470人以上を標本として抽出すると、標本誤差0.02以内に収めるという目標が達成される見込みであることがわかります。
ただし、これは単純無作為抽出で標本抽出を行い、回収率が100%であると仮定したときの数字であるのには注意が必要です。
多段抽出を行うと、概ね段数のルートに比例して標本誤差が大きくなることが知られています。例えば二段抽出であれば、εを2の平方根で除して調整する必要があります。結果、より多くの人を対象としなければなりません。
また、回収率が100%からほど遠いと予想されるなら、計算されたnに回収率の逆数(例えば50%なら1/0.5=2)を掛けて、さらに多くの人を対象者として抽出しなければならなくなります。
2-1 標本設計 まとめ
- 母集団から無作為抽出により対象者を選ぶことで、代表性が確保され、一般化ができるようになる。
- 標本調査のポイントは無作為抽出であり、目的・予算・母集団に合わせて抽出方法を選択する。
- 目標とする標本誤差を決めれば、計算によって調査人数(標本規模)を見積もることができる。
執筆・監修:東京大学社会科学研究所 教授 三輪 哲




