感染源の特定
疫学研究とは、疾病や健康状況などについて、特定の集団を対象として、その原因や発生条件を統計的に明らかにする研究です。
例えば、ある集団において病気が発症した場合、まず、病気が発症したグループと発症していないグループを選び、過去に病気の原因と考えられる要因にどれ位さらされたのか(疫学の分野では「曝露したか」といいます。)を調べます。そして、2つのグループについて、病気の要因にさらされた人とさらされていない人の割合の違いが統計学的に意味があるかを評価し、病気と要因の関係を調べていきます。
ここでは、集団食中毒が発生した場合を例として、食中毒の原因と疑われる食事を突き止めるまでを紹介したいと思います。
ある地域で開催されたパーティーで30人の食中毒患者が発生したため、食中毒を発症した人たちに対して摂取した飲食物に関する調査を行ったとします。その結果、食中毒を起こした30人はパーティーの出席以外に、共通の飲食物を摂取する機会がないことが分かり、そのパーティーが食中毒の原因と考えられたとします。
そこで、パーティーで出された複数の飲食物(A~D)について、患者30人とその他の出席者(食中毒を発症しなかった人)から無作為の選んだ35名について調査した結果、表のとおりになったとします。
| 食中毒を発症した人(計30人) | 食中毒を発症しなかった人(計35人) | |||
|---|---|---|---|---|
| 飲食物 | 摂取した | 摂取しなかった | 摂取した | 摂取しなかった |
| A | 15 | 15 | 12 | 23 |
| B | 16 | 14 | 15 | 20 |
| C | 13 | 17 | 13 | 22 |
| D | 20 | 10 | 11 | 24 |
この表から食中毒の原因と疑われる要因(飲食物)を見つけるために用いられるのが「オッズ比(※1)」と呼ばれる関係の強さを示す指標です。
表1の場合のオッズ比は、

となります(図参照)。
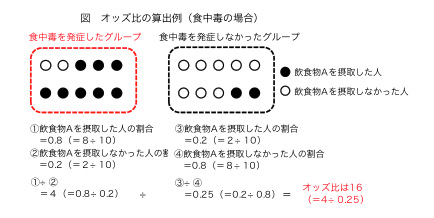
この比は食中毒を発症した集団と食中毒を発症しなかった集団について、原因と疑われる飲食物を摂取した人の割合を比較することで、2つの集団の飲食物による食中毒の起こりやすさを示していることになります。そのため、オッズ比が1以上となった飲食物は、食中毒を引き起こす可能性が高いということになるわけです。(食中毒は飲食物を摂取した時に起こるので、原因となる飲食物の場合は、オッズ比が1より大きくなるはずです。)
また、オッズ比が1の場合は、食中毒を起こした集団と起こさなかった集団では、食中毒の起こりやすさが変わらないということになり、その飲食物は食中毒の原因である可能性は低いと考えられます。
では、実際にオッズ比を求めてみます。飲食物Aを摂取したことよる食中毒のオッズ比は、
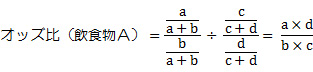
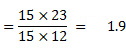
a:飲食物Aを摂取して、食中毒を起こした人 b:飲食物Aを摂取しなくても、食中毒を起こした人
c:飲食物Aを摂取しても、食中毒を起こさなかった人 d:飲食物Aを摂取していなく、食中毒を起こさなかった人
同様に他の飲食物についてもオッズ比を求めると、表2のとおりになります。得られたオッズ比は推定値であるため、真の値はその周辺にあることが考えられます。表2の信頼区間95%は、95%の確率で真の値が存在する範囲を示しています(※2)。このため、信頼区間の下限値が1より大きければ、統計的に有意(意味があること)な関係があると判断されます(図2)。
以上のことから、食中毒の原因となる飲食物を判断するためには、「オッズ比が1より大きい」と「信頼区間の下限値が1より大きい」という2つの条件を同時に満たすことが必要となるわけです。
| 飲食物 | オッズ比(信頼区間95%) |
|---|---|
| A | 1.9(0.7-5.2) |
| B | 1.5(0.6-4.1) |
| C | 1.3(0.5-3.5) |
| D | 4.4(1.5-12.4) |
表2から、各飲食物を摂取したことよる食中毒のオッズ比を比較すると、3つの飲食物でオッズ比は1をやや上回っていますが、95%信頼区間の下限が1を下回っています。しかし、飲食物Dではオッズ比が4.4となっており、95%信頼区間の下限が1を上回っているので、食中毒の原因となった飲食物は、飲食物Dではないかと考えることができるわけです。
なお、表2では原因となった飲食物Dを摂取していなくても食中毒になった人がいますが、これは、調理の過程や盛りつけの際に飲食物Dによって他の食品の一部に食中毒菌がつくことなどが考えられるため、食中毒の原因と考えられる飲食物を摂取していなくても食中毒になる場合があるためです。
(※1) 仮にパーティーの出席者全員の調査が可能な場合は、相対危険度という指標が使われますが、全員の調査が不可能な時にはオッズ比が使われます。なお、上の例の場合でいうと、相対危険度は「飲食物Aを摂取した人」と「飲食物Aを摂取しなかった人」の食中毒の発生頻度を比で表したものになります。
また、ある事象が確率Pで発生するとき、この事象が発生しない確率は1-Pとなり、このとき、P/(1-P) をオッズといいます。オッズ比は、2つのオッズの比を取ったものとなります。
(※2)詳しい式の導出過程は省略しますが、表1についてオッズ比の95%信頼区間の上限値及び下限値は、次式で求めることができます。
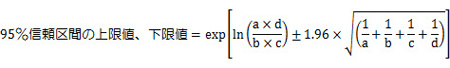
a:飲食物を摂取して、食中毒を起こした人 b:飲食物を摂取しなくても、食中毒を起こした人 c:飲食物を摂取しても、食中毒を起こさなかった人 d:飲食物を摂取していなく、食中毒を起こさなかった人
参考文献
感染症流行調査の基本、国立公衆衛生院疫学部 簑輪眞澄
