2変数のカテゴリデータがあれば、より詳細な検討ができるようになります。2つのカテゴリ変数を組み合わせて同時に集計することを、クロス集計といいます。クロス集計をしてできあがる表のことを、クロス集計表、あるいは分割表と呼びます。

クロス集計表では、表側（ひょうそく、表の左側のこと）と表頭（ひょうとう、表の上側のこと）とに、それぞれ変数が配置されます。そのようにすることで、2つの変数への回答を一度にみることができるわけです。クロス集計表の例を、ここでみてみましょう。

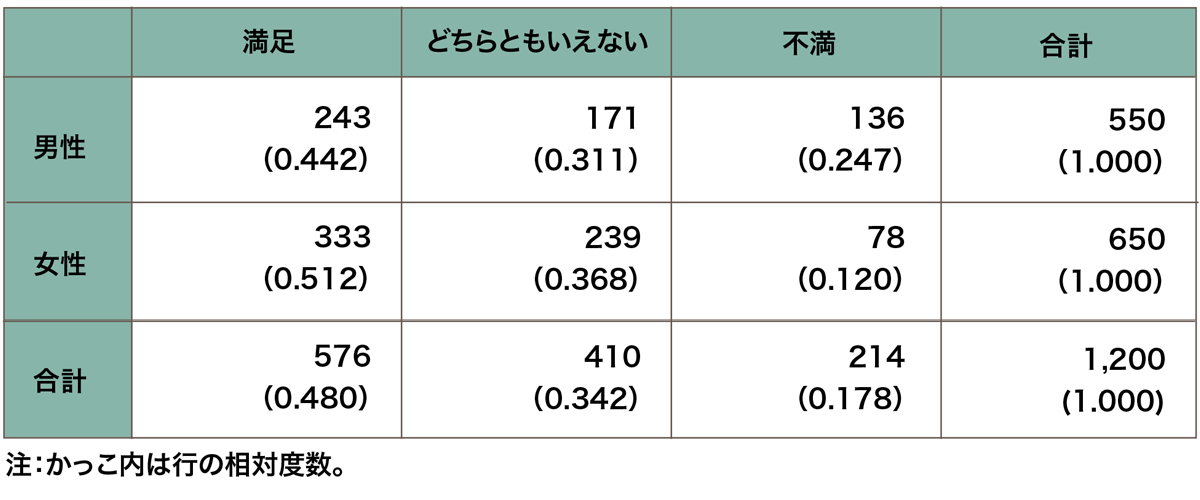
クロス集計表においても、横方向のまとまりを行、縦方向のまとまりを列と呼びます。各々の行と列とが交差する箇所のことは、セルと呼びます。
そして、それぞれのセルには、2つの変数へと回答した人数が、度数としてあらわされます。上の例だと、例えば1行1列は度数が243となっています。つまり、「男性」であり、なおかつ「生活に満足」と回答した人が243人だったことがわかります。

また、合計の度数のことを、周辺度数といいます。
クロス集計表では、行の周辺度数（横方向の合計人数）、列の周辺度数（縦方向の合計人数）、総度数（全体での合計人数）と、3種類の周辺度数があります。

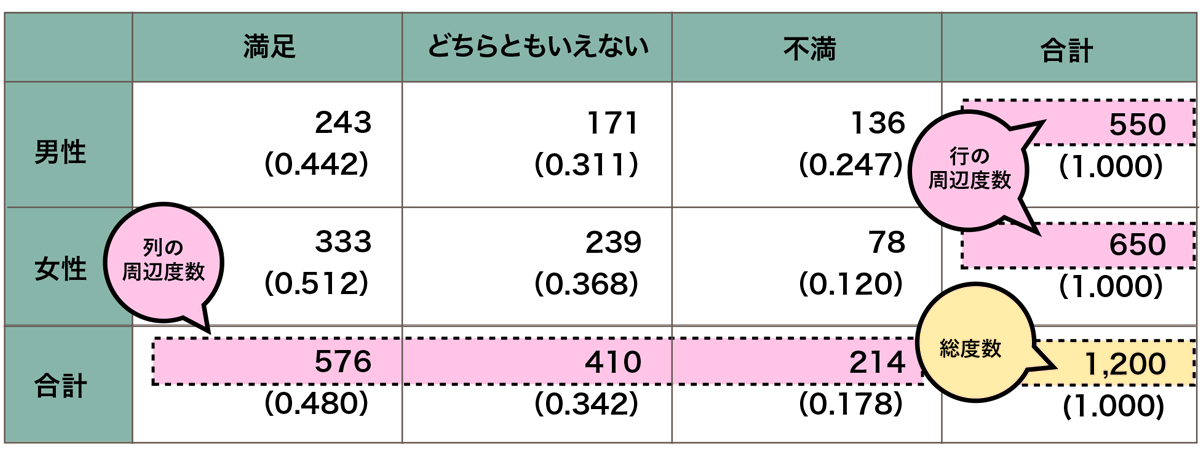
クロス集計表でも、相対度数を計算して、割合を比べることが行われます。相対度数は、セル度数を周辺度数で割ることで求められます。なぜそうするかというと、カテゴリごとに合計人数が異なるため、単純に度数の多い・少ないだけをみるのでは回答傾向の比較がしにくいからです。

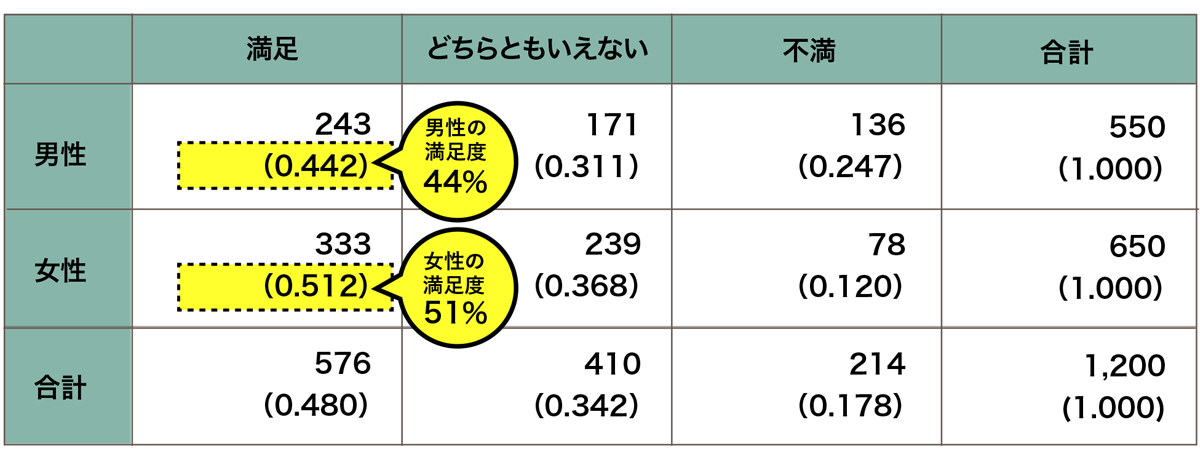
周辺度数が3種類あるため、相対度数も3種類ありえますが、もっともよく用いられるのは、行の周辺度数を分母とした相対度数です。これは、関心のある意識項目を表頭に、説明要因とする属性項目を表側に配置することが慣例的に多いことによります。そのようなときに行方向の相対度数を出せば、例えば、上記の例だと「男性の満足度が44%で、女性の満足度は51%だから、女性のほうが高い」などと、集団間での回答傾向の違いを読み取りやすいのです。

クロス集計表の使い方としては、ブレイクダウン集計のために行うか、関連の検証のために行うかに、大別されます。

ブレイクダウン集計とは、関心のある意識項目の度数分布を明らかにしたのに続き、度数分布を下位集団ないし属性ごとに分けてみていく分析方針をさします。

関連の検証とは、2つの意識項目や、属性項目と意識項目など、2つの変数のあいだの関連の向き、強さ、形状を読み解くために行う分析方針をさします。クロス集計表で関連の有無を判定する方法に、さまざまな統計的検定を用いることができます。また、関連の向きや強さをとらえる連関係数（属性相関係数）もいろいろ提唱されています。これらはやや難解なので、説明は専門書に譲り、ここでは割愛します。

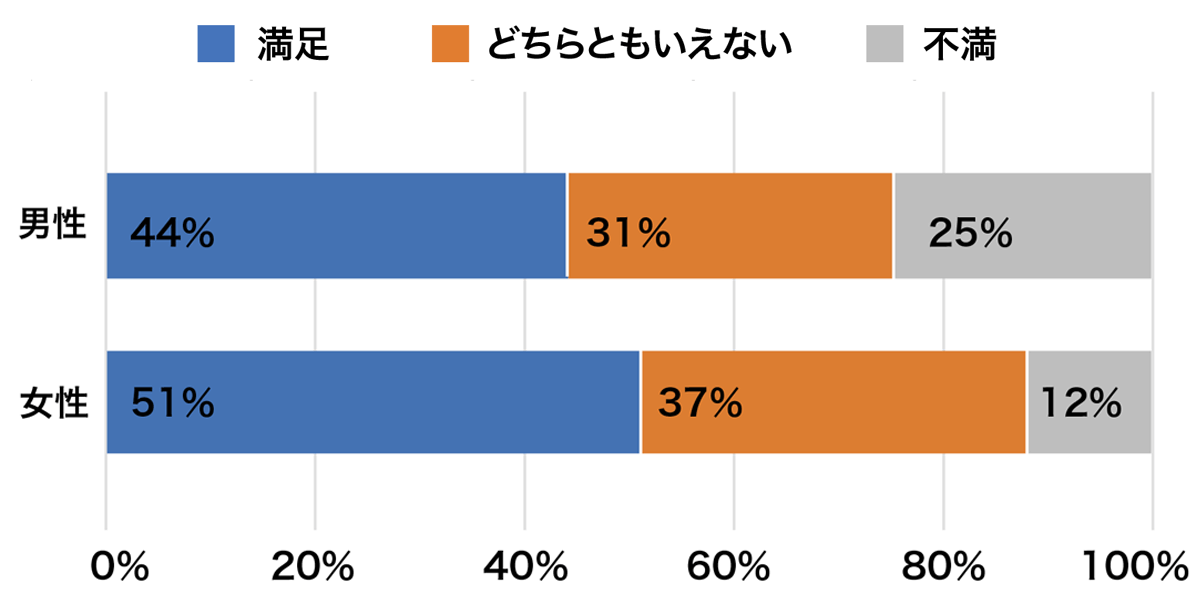
クロス集計の結果を視覚的に表現するには、グラフを利用すればよいです。ここでも、帯グラフの利活用がおすすめできます。
先ほどのクロス集計表の出力例をもとに、帯グラフ化したものを以下に示します。各カテゴリの相対度数の大きさが帯の長さであらわされ、それぞれの帯が比較すべき集団を示しています。表よりも、グラフの方が、結果を直感的に理解しやすいことが納得できるのではないでしょうか。