迷惑メールの判別
電子メールが広く普及した現在、世界中で送られている電子メールの多くは、迷惑メール(スパムメール)だといわれています。受信した電子メールについて、ユーザー自身が必要なものと不要なものに振り分けることは、電子メールが多い場合、非常に大変です。
このため、多くのメールソフトでは、スパムメールを効率的かつ自動的に排除するために、メールのフィルタリング機能が使われています。あるメールを受信したとき、これが通常のメールなのか、スパムメールなのかを判別するフィルタリング機能には、電子メールのタイトルや本文中の単語の出現する確率によって両者を判定する統計的な手法などが用いられています。
ここでは、ベイズ理論を応用した電子メールのフィルタリングとして「ベイジアンフィルタ」について紹介したいと思います。
ベイズ理論は、18世紀のイギリスの牧師トーマス・ベイズの「確率問題の解決のためのエッセイ(1763年)」を起源とする理論であり、過去に起きた事象の確率を利用して、未来に起こる事象の確率を予測する理論です。
ベイズ理論を応用したベイジアンフィルタは、まず、電子メールの特徴を抽出するため、過去の受信メールを通常のメールとスパムメールに分類して、データベースに格納しておきます。そして、新たに受信した電子メールについて、その内容(文章)を単語に分割(※1)し、データベースの情報(過去の受信メールの情報)を利用し、各単語について、
1.スパムメールと判明しているとき、このメールが該当単語を含む確率(条件付き確率)
2.スパムメールでない(通常メール)と判明しているとき、このメールが該当単語を含む確率(条件付き確率)
を計算します。そして、ベイズの定理を用いて、「該当単語を含むメールがスパムメールである確率」を求め、この確率が大きければ、受信メールはスパムメールに分類されます(※2)。さらに、分類された電子メールの情報は、新たに受信した電子メールをスパムメールかどうか判別する際に利用されます。
このように、ベイジアンフィルタは、あらかじめ蓄積された情報を用いて、新たな事象を判別しているため、判別を繰り返すことで、フィルタの精度の向上やユーザーの趣向に合った判別が望めることになります。
ベイジアンスパムフィルタ(イメージ)
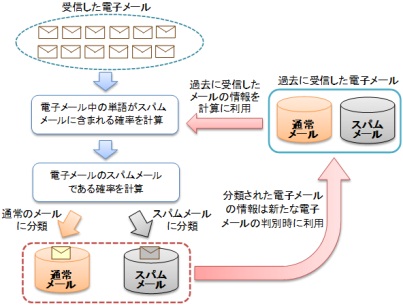
ベイズ理論は確率論・統計論のみならず、ここで紹介したスパムメールのフィルタリング機能の他にも、経済学、情報科学、心理学、人工知能、行動科学、情報論などの多くの分野において応用がされています。
(※1) 単語(専門的には「トークン」と呼ばれます。)の分割に関して、英語は単語間が空白で区切られているため、基本的には単語を単位として、トークンに分割されます。一方で、日本語は空白で区切られていないため、連続する漢字やカタカナに着目してトークンに分割する方法など、分割にはいくつかの方法があります。
(※2) ベイズの定理を用いて計算する際は、条件付き確率のほかに「これまでの受信した通常メールとスパムメールの件数の割合(事前確率と呼ばれます。)」が必要となります。
参考文献
・ベイズな予測―ヒット率高める主観的確率論の話、宮谷 隆、岡嶋 裕史、リックテレコム
・史上最強図解 これならわかる!ベイズ統計学、涌井 良幸、涌井 貞美、ナツメ社
ベイズの定理
ベイズの定理は、乗法定理から得られます。乗法定理とは、次の定理です。
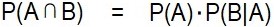 ・・・・・①
・・・・・①
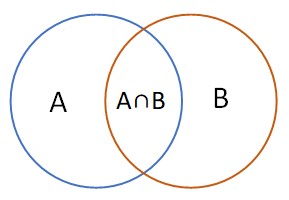
P(A)、P(B)はある事象A、Bが起こる確率、P(B|A) はAが起こったときにBが起こる確率を表します。
①式の右辺を変形させて

また、AとBの役割を変えて、Bが起こったときにAが起こる確率 (P(A|B)) で表すと、次のようにも書くことができます。

これら2つの式は左辺 P(A∩B) が共通なので、次の式が成り立ちます。
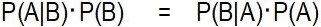
P(B)≠0と仮定し、両辺をP(B)で割ると、P(A|B) は次の式で表せます。
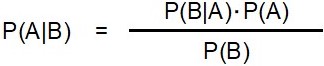 ・・・・・②
・・・・・②
これが「ベイズの定理」です。
P(A) を事象Bが起きる前の事象Aが起きる確率として「事前確率」、P(A|B) を事象Bが起きた後で事象Aが起きる確率として「事後確率」と呼びます。
また、ベイズの定理は下のような展開式で使われます。
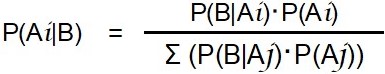 ・・・・・③
・・・・・③
ベイズ定理の利用例
(検査で陽性になったけど、本当に病気なの?)
架空の病気の検査を例に、ベイズの定理の説明をします。ある病気を発見する検査について、次のことが分かっています。
・日本で、ある病気にかかっている人は、0.5%である。
・病気にかかっている人を検査すると、90%の人が陽性になります。
・病気にかかっていない健康な人を検査すると、2%の人が陽性になります(偽陽性)。
ここで、日本国内に住むTさんがこの検査を受けて陽性になったとき、Tさんが本当に病気である確率は、どのくらいでしょうか。
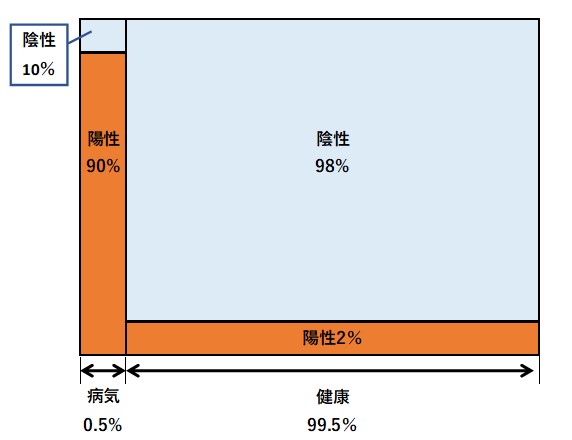
病気にかかっている事象(病気)をA1、病気にかかっていない事象(健康)をA2、検査で陽性になる事象をBとすると、それぞれの確率は、次のようになります。
・病気にかかっている(病気)確率:P(A1)=0.005
・病気にかかっていない(健康)確率:P(A2)=0.995
・検査が陽性で病気の確率:P(B|A1)=0.90
・検査が陽性で健康の確率:P(B|A2)=0.02
③のベイズ定理の変形式に上記の条件を当てはめると

となり、陽性と判定されても、実際に病気である確率は、18.4%です。陽性と判定されると、「自分は病気かもしれない」と心配しがちですが、「検査が陽性で病気の確率」90%と比べると、意外に小さな確率であることが分かります。
実際には「検査が陽性で健康(偽陽性)」が多いため、「検査が陽性で病気(真の陽性)」をはるかに上回ってしまいます。
付録
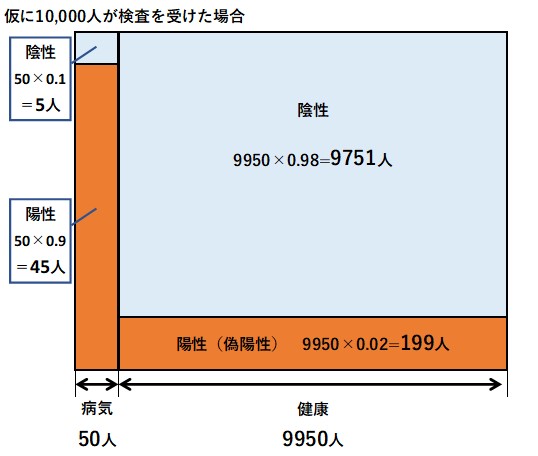
ベイズの定理は難しいと思われがちですが、下記のように面積図に人数を当てはめると簡単に計算ができます。
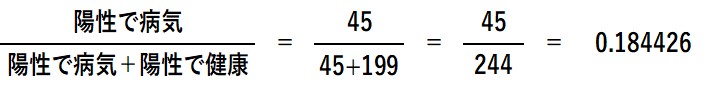
参考文献
・涌井良幸、涌井貞美(2010) 『EXCELでスッキリわかる ベイズ統計入門』 日本実業出版社
・涌井良幸、涌井貞美(2012) 『史上最強 図解 これならわかる!ベイズ統計学』 ナツメ社
・小島寛之(2015) 『完全独習 ベイズ統計学入門』 ダイヤモンド社
