統計的推定と統計的仮説検定

統計的推定

推定の方法

　推定は、母集団の特性値（平均や分散など）を標本のデータから統計学的に推測することで、推定には点推定と区間推定があります。点推定で推定するのは1つの値で、区間推定ではある区間（幅）をもって値を推定します。

点推定

　点推定は、母集団の平均や分散などの特性値を、1つの値で推定します。
　例えば母平均（母集団の平均）の点推定は、大数の法則から標本の大きさが大きくなるほど、標本の平均は母平均に近づくため、標本の平均が母平均の推定値となります。ただし、実際の標本の大きさは無限に大きいものではないため、母平均の推定値は、実際の値と完全には一致しないことが考えられます。そのため、推定量がどのくらい正しいものかを表す指標に、標準誤差があります。
　標準誤差は推定量の標準偏差であり、標本から得られる推定量そのもののバラつきを表すものです。標本平均の標準誤差は母集団の標準偏差を用いて表すことができますが、多くの場合、母集団の標準偏差は分からないので、標本から得られた不偏分散の正の平方根sを用いて推定します。

　𝑛：標本の大きさ、  を標本の個々のデータ とした場合、標準誤差は以下の数式で求めることができます。

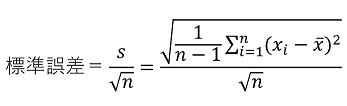
　標本の大きさが大きくなるほど標準誤差は小さくなります。

区間推定

　区間推定は、母集団が正規分布に従うと仮定できる場合に、標本のデータを用いて母平均などの推定量を、1つの値ではなく、入る区間（幅）で推定します。推定する区間を信頼区間と呼び、「90%信頼区間」「95%信頼区間」「99%信頼区間」などで求めます。
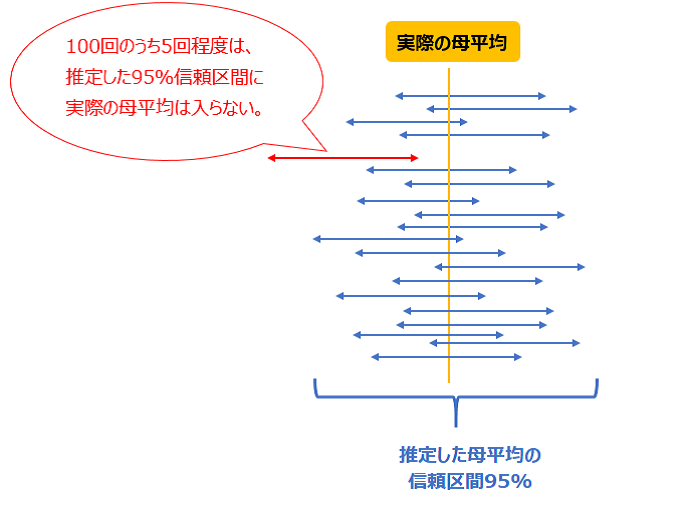
　例えば「95%信頼区間」で求めた場合、「母集団から標本をとりだし、その標本から母平均の95%信頼区間を求める」ことを100回実施したとき、95回程度はその区間内に母平均が入る」ことを表します^※。

　※母平均は知られていないだけで確定した値なので、得られた標本のもとで母平均がその区間内にある確率が95%という意味ではないことに注意してください。

統計的仮説検定

　検定は、母集団に関するある仮説が統計学的に成り立つか否かを、標本のデータを用いて判断することで、以下の①～④の手順で実施します。
① 仮説を設定する
② 有意水準を決定する
③ 検証する
④ 結論を導く

　あるハンバーガーチェーン店では、Ⅿサイズのフライドポテトは135gと公表されている。実際には、フライドポテトの重量を逐一測って提供していてはサービスに時間がかかるため、店舗スタッフが目分量で判断していることが多い。そこで、本当にフライドポテトの重量が公式発表の135gとなっているのかどうか疑問がわく。ここでは、「駅前のハンバーガー店のフライドポテトの重量が公表値の通りか」を検証するため、統計的仮説検定を実施してみましょう。

①仮説を設定する

　「駅前のハンバーガー店のⅯサイズのフライドポテトの重量が公表されている通りかどうか疑わしい」という仮説（対立仮説）を考え、これを検証するために、この仮説とは相反する仮説（帰無仮説）を設定します。

帰無仮説	駅前のハンバーガー店のフライドポテトの重量が公表値の135gのとおりである。
対立仮説	駅前のハンバーガー店のフライドポテトの重量が公表値の135gではない。

※公表値の135gとは、駅前のハンバーガー店が販売している全フライドポテトの平均が135gと考えます。

②有意水準を決定する

　有意水準とは、帰無仮説が間違っていると判断する（帰無仮説を棄却する）基準となる確率のことです。有意水準0.05に設定した場合、5%以下の確率で生じる現象は、非常にまれなことであるとします。有意水準は、0.05や0.01が多く使われています。ここでは、有意水準0.05とします。

③検証する

　帰無仮説が正しいと仮定した上でのデータが実現する確率を、「推定検定量」に基づいて算出します。
　今、高校生のグループが手分けして、駅前のハンバーガー店で、Mサイズのフライドポテトを10個購入し、各フライドポテトの重量を計測した結果が、以下の表のようになったとします。

購入した 10 個のフライドポテトの重量（各重量をX1、Ｘ２…X10 とします。）

120g

124g

126g

130g

130g

131g

132g

133g

134g

140g

　まずは、検定統計量Zをもとめてみましょう。駅前のハンバーガー店で販売しているフライドポテトの重量は正規分布にしたがっているとすると、購入した10個のフライドポテトの重量の平均、つまり標本平均はN(μ,σ²/10)に従います。μは、ハンバーガー店で販売しているフライドポテト全ての平均、つまり母平均で、σ²は母分散を示しています。帰無仮説（フライドポテトの重量は135gであるという仮説）が正しいと仮定すると、母平均μは135であると仮定でき、母分散が既知でσ²=36とした場合、検定統計量Zは以下のように求めることができます。（ は、購入した10個のフライドポテトの重量の平均、つまり標本平均の130g、nは購入したフライドポテトの個数、つまり標本の大きさである10を示します。）

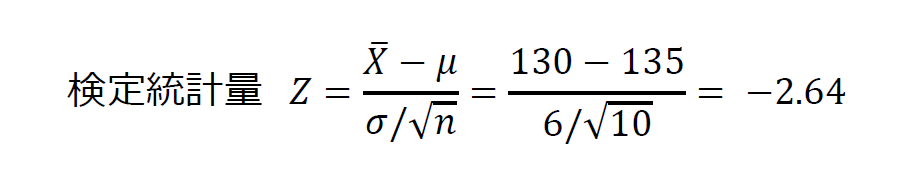
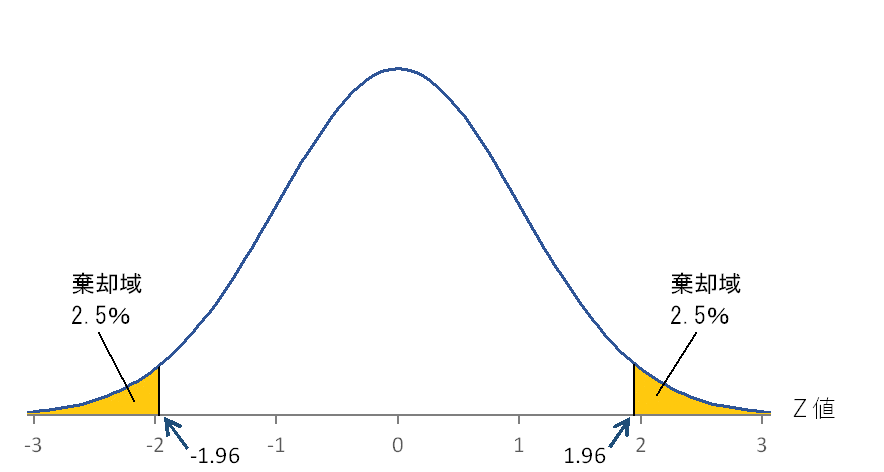
　この検定統計量Z（-2.64）が、有意水準0.05の境界線（-1.96）と等しいかそれより小さな値（Zが正の数の場合には1.96より大きな値）になる確率をP値や有意確率などと呼びます。

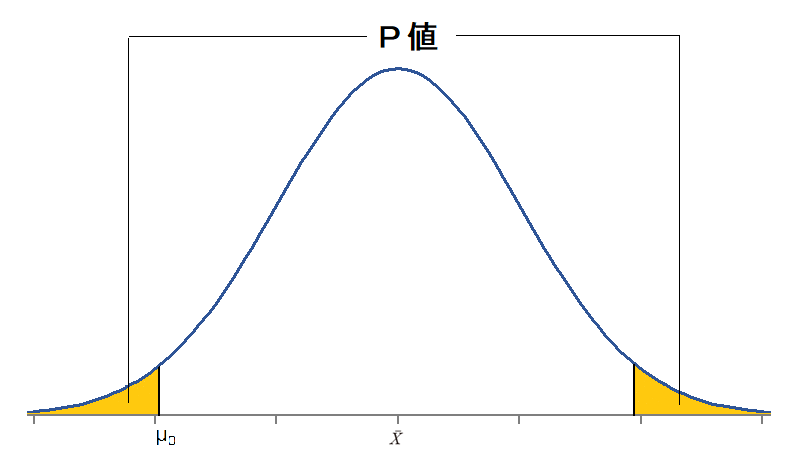
　次にP値をもとめてみましょう。

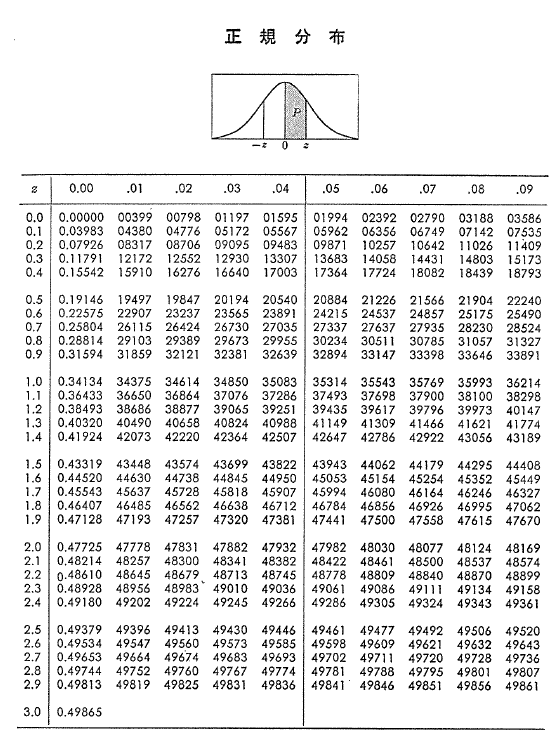
　対立仮説「駅前のハンバーガー店のフライドポテトの重量が公表値の135gではない。」は、公表値の135gよりも重い場合と軽い場合の両方が考えられますが、「公表値の135gではない」は重い場合でも軽い場合でもよいため、両側検定と呼ばれる方法を使用します。検定統計量Zは標準正規分布に従うため、標準正規分布表から検定統計量2.64に対応する値を確認すると(0.5－0.49585)＝0.00415、両側検定では2倍した値がP値となるので0.0083がP値となります。P値が②に決めた有意水準0.05よりも小さいことから、設定した仮説のもとで観察された事象が起こることは非常にまれなことであると判断できます。

④結論を導く

　検証した結果、設定した仮説「駅前のハンバーガー店のフライドポテトの重量が公表値の135gのとおりである。」は正しいとは言えないと分かります（帰無仮説を棄却）。よって、対立仮説である「駅前のハンバーガー店のフライドポテトの重量が公表値の135gのとおりではない。」が正しいと判断することできます。
　このように、仮説検定では帰無仮説が棄却されれば、帰無仮説とは相反する対立仮説を採択することになります。