統計をグラフにあらわそう
統計をグラフにあらわそう
統計は、データを集めて集計しただけでは、単なる数字の集まりであり、そこから何が読み取れるか必ずしも明らかではありません。
統計を作成するときは、必ず、「○○について知りたい!」という目的があるはずですから、得られた結果を、その目的に合わせて上手に使うことが重要です。グラフは、結果を視覚的に表す便利な道具であり、グラフをうまく使うことによって、自分の考えていることを相手に的確に伝えることができます。
グラフにはいくつかの種類があり、それぞれ、得手・不得手があります。自分が伝えたい目的に応じて、適切なグラフを使うことにより、説明力もぐっと高まります。ここでは、そういったグラフの種類やそれぞれの用途、注意点について説明します。
- 棒グラフ
- 棒の高さで、量の大小を比較する。
- 折れ線グラフ
- 量が増えているか減っているか、変化の方向をみる。
- 円グラフ
- 全体の中での構成比をみる。
- 帯グラフ
- 構成比を比較する。
- ヒストグラム
- データの散らばり具合をみる。
- レーダーチャート
- 複数の指標をまとめてみる。
- 散布図
- 2種類のデータの相関をみる。
- 箱ひげ図
- データの散らばり具合をみる。
- 三角グラフ
- 3つの量からなる構成比をみる。
- 量の大小をあらわすときには、どのグラフを使えばいいですか?
- 棒グラフを使えば、量の大小を、棒の高さであらわすことができます。
- 増えている、減っているといったことをあらわすには、どのグラフを使えばいいですか?
- 折れ線グラフを使えば、線の傾きで、増減をあらわすことができます。
- 割合をあらわすときには、どのグラフを使えばいいですか?
- 円グラフや帯グラフを使います。三角グラフを使うこともあります。
- データの散らばり具合をあらわすときには、どのグラフを使えばいいですか?
- ヒストグラムや箱ひげ図を使います。
- 複数の指標をまとめてあらわすときには、どのグラフを使えばいいですか?
- 棒グラフや折れ線グラフでもあらわすことができますが、レーダーチャートを使えば、平均と比較したときにどの項目が大きいか等をわかりやすくあらわすことができます。
- 2つの量に関係があるかどうかをあらわすときには、どのグラフを使えばいいですか?
- 散布図を使います。
棒グラフ
-
たとえば・・・
日本列島は東西・南北に長いため、どんなものを食べているか、地域によってかなり特色があります。ここでは、総務省統計局「家計調査」を使って、たらこの消費量にどのような地域特色があるか、みてみましょう。
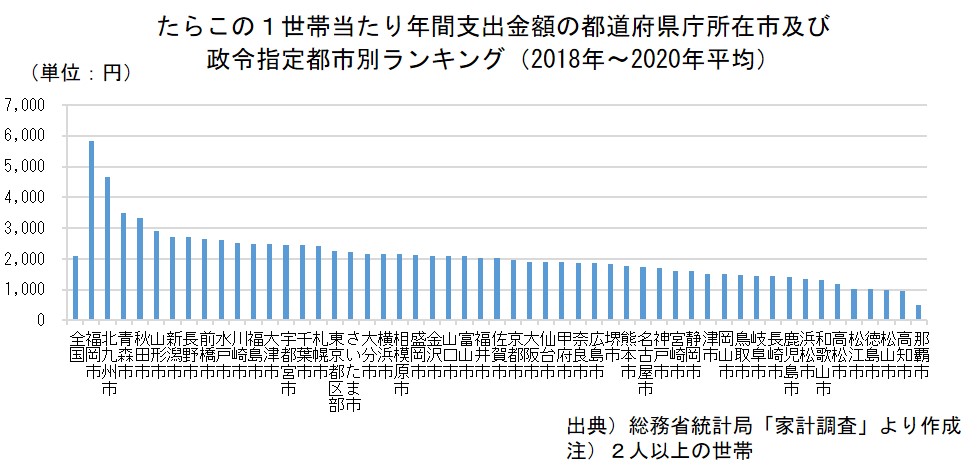
これをみると、福岡県の福岡市、北九州市でのたらこ購入量が飛び抜けて大きいことが一目でわかりますね。福岡は「辛子明太子」で有名ですから、ご家庭でたらこを買う量も多い、ということでしょう。(「世帯」という言葉は耳慣れないかも知れませんが、「いっしょに住んでいる家族のこと」と思って下さい。)
-
どんなときに使うの?
棒グラフは、縦軸にデータ量をとり、棒の高さでデータの大小を表したグラフです。(稀に縦横が逆の場合もあります。)
データの大小が、棒の高低で表されるので、データの大小を比較するのに適しています。
上記の例だと、福岡市、北九州市でのたらこ購入量が他と比べてどんなに多いか、一目でわかりますよね。 -
気をつけることは?
棒グラフを描くときに、データをどの順に並べるかは、とくに決まりはありません。ただし、あまり意味もなく並べてもグラフが見にくいので、
- データの多い順(または少ない順)に並べる。・・・上記の例
- 都道府県データの場合、北から順に並べることもある。
- 五十音順に並べる。
- 横軸が年や月といった時間軸である場合、時間の順に並べる。
- 質問に対する回答を並べる場合、質問票の順と同じ順に並べる。
などの方法をとります。
-
その他には?
先ほど紹介したのは、棒グラフのうちでも、もっとも単純なものですが、もっと複雑な棒グラフもあります。
そういった複雑なグラフのいくつかを紹介しましょう。-
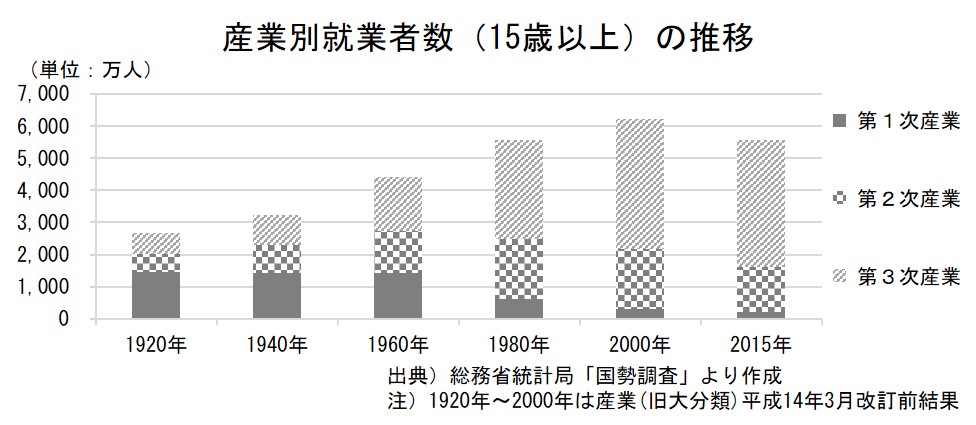
積み上げ棒グラフ
1本の棒に、複数のデータを積み上げて表示したもの。
-
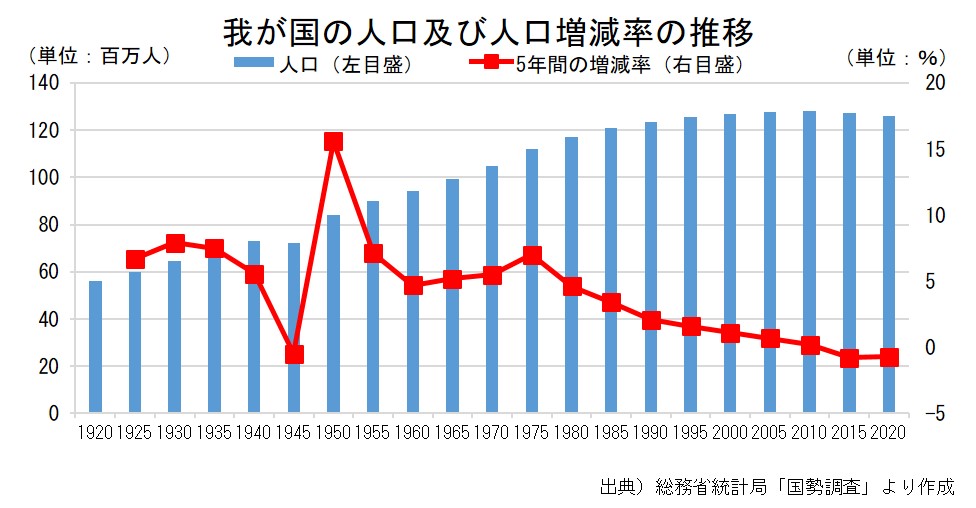
棒グラフと折れ線グラフの複合グラフ
-
-
やってみよう
総務省統計局「家計調査」では、たらこ以外の品目についてもデータを掲載しているので、それらについてもグラフを描いてみましょう。
折れ線グラフ
-
たとえば・・・
たまごは、昔は「物価の優等生」と呼ばれ、様々なものの値段が変動する中で価格が安定していたのですが、最近では、「たまごの値段が上がった」というニュースも見かけるようになりました。たまごの値段の変化を、総務省「消費者物価指数」で見てみましょう。
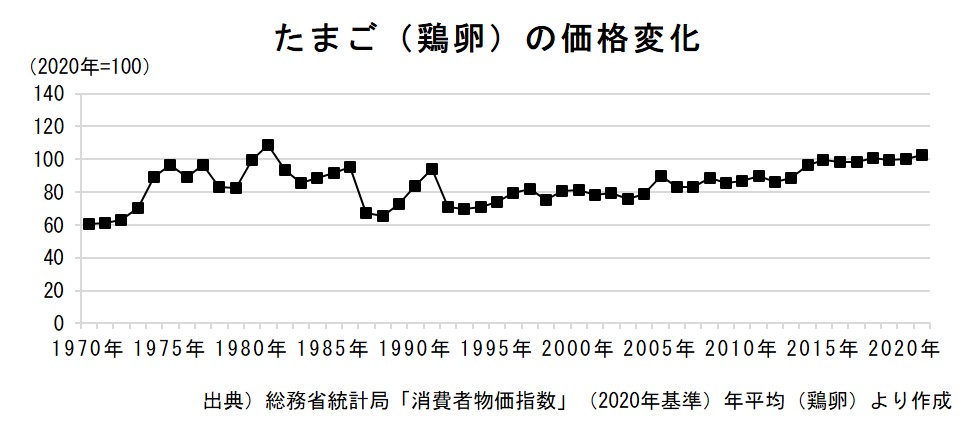
ここでは、たまご(鶏卵)の価格の年平均をグラフにしました。ここで使った「消費者物価指数(2020年基準)」は、2020年の平均価格がちょうど100になるように計算されています。
これをみると、たまごの値段が上下していることがわかります。ニワトリの飼料は輸入穀物に頼っていること、養鶏場の暖房等の費用もかかることから、たまごの価格も、国際的な穀物価格や原油価格の動向に左右されやすい、という側面もあります。
-
どんなときに使うの?
折れ線グラフは、横軸に年や月といった時間を、縦軸にデータ量をとり、それぞれのデータを折れ線で結んだグラフです。線が右上がりならその期間はデータが増加(上昇)、右下がりならデータが減少(下降)していることになるので、データの増減を見るのに適しています。
-
気をつけることは?
折れ線グラフでは、複数のデータを一つのグラフに重ねて描き、「こちらのデータは増加しているが、こちらは減少」という比較をすることがありますが、その場合、線の区別がつきやすいよう、線を色分けしたり、実線と破線を使い分けたりします。
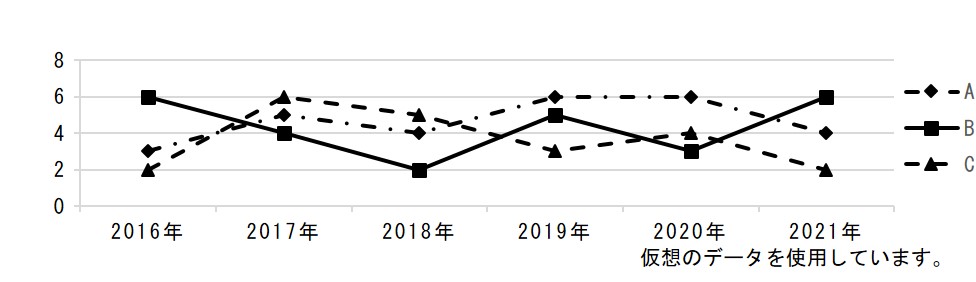
また、折れ線グラフの縦軸の目盛りは、ゼロから始めるのが普通ですが、あまり数字に変化がなくて見にくいときは、縦軸に波線を入れて途中を省略することもあります。
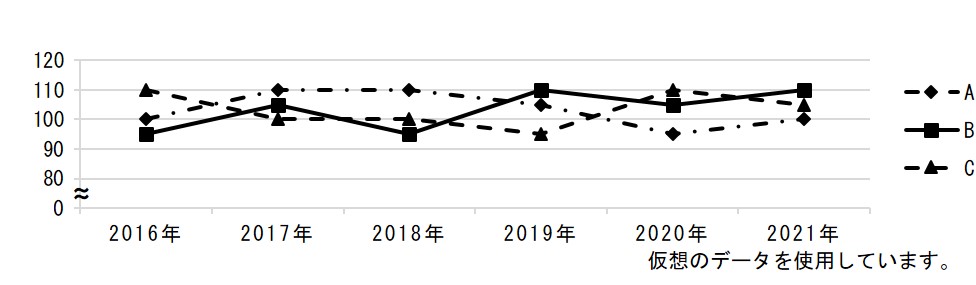
また、Cだけ数値が大きく違っていて、一つのグラフに描きにくい、という場合もあります。その場合は、Cだけ右目盛りで表示する、ということにして、一つのグラフに収めることもできます。
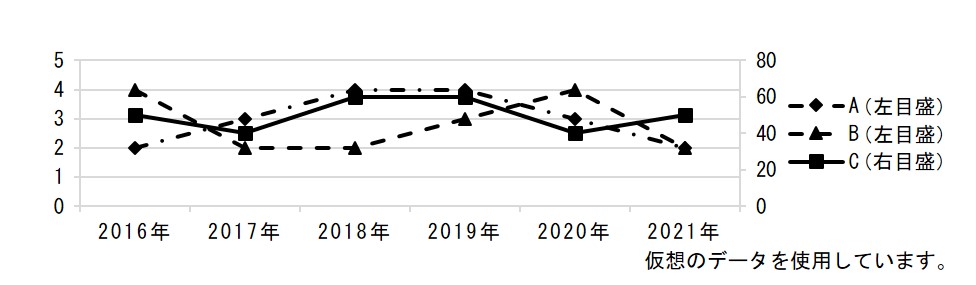
-
やってみよう
総務省統計局「消費者物価指数」では、その他の様々な品物の価格を調べています。
たまご以外のいろいろな品物やサービスの価格について調べ、グラフにしてみましょう。
円グラフ
-
たとえば・・・
近年、我が国では日本国内に住む外国人の人口が増えてきています。いったいどの国の人々が多く住んでいるのでしょうか。
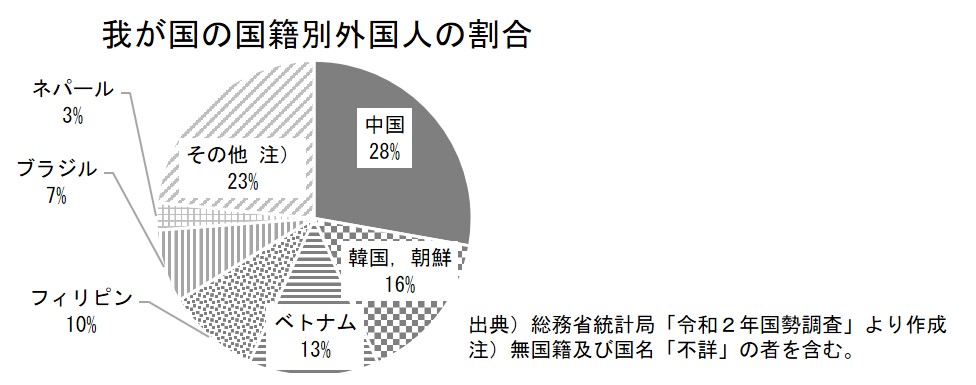
中国、韓国、朝鮮などのアジア圏の人々の人口が全体の半分以上を占めていることがわかります。
-
どんなときに使うの?
円グラフは、円を全体として、その中に占める構成比を扇形で表したグラフです。
扇形の面積により構成比の大小がわかるので、構成比を示すのに使われます。 -
気をつけることは?
データは、時計の針の12時の位置から時計回りに、大きい順に並べます。
「その他」はいくら大きくても、一番最後に表示します。あまり扇形が小さくなるとグラフが見にくくなるので、構成比が小さいものは、まとめて「その他」にしてしまった方がよいでしょう。
なお、「○○に賛成ですか」のような質問に対する回答を円グラフに表示する場合など、必ずしもデータの大きい順に並べないこともあります。「賛成」と「どちらかといえば賛成」を合わせて過半数かどうか、ということが一目でわかるようにする方が便利だからです。
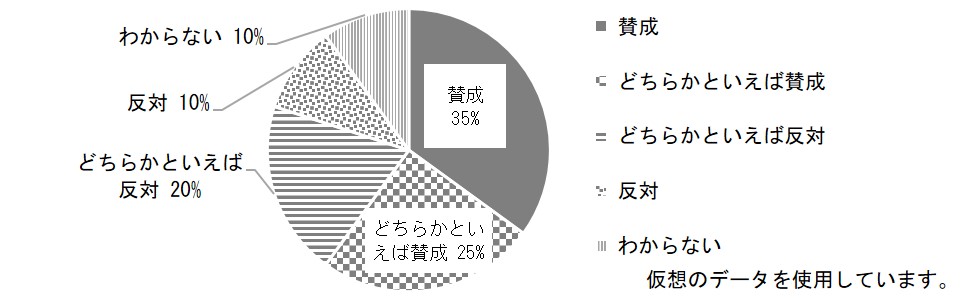
円グラフを描くときは、合計が100%になるようにします。上の例で「わからない」を除いてしまうと合計が100%にならなくなりますが、それで円グラフを描いてはいけません。
また、複数回答を認める質問の場合、合計が100%を超えますが、このような場合も円グラフにしてはいけません。
-
やってみよう
総務省統計局「家計調査」では、ご家庭で、どのようなものを買っているか、調べています。円グラフを描いて、どのようなものにお金を使っているか、見てみましょう。
帯グラフ
-
たとえば・・・
「最近、農業をする人の割合が減ってきた」との話を聞きますが、総務省「国勢調査」で、第1次産業・第2次産業・第3次産業別の就業者数の割合の変化をみてみましょう。
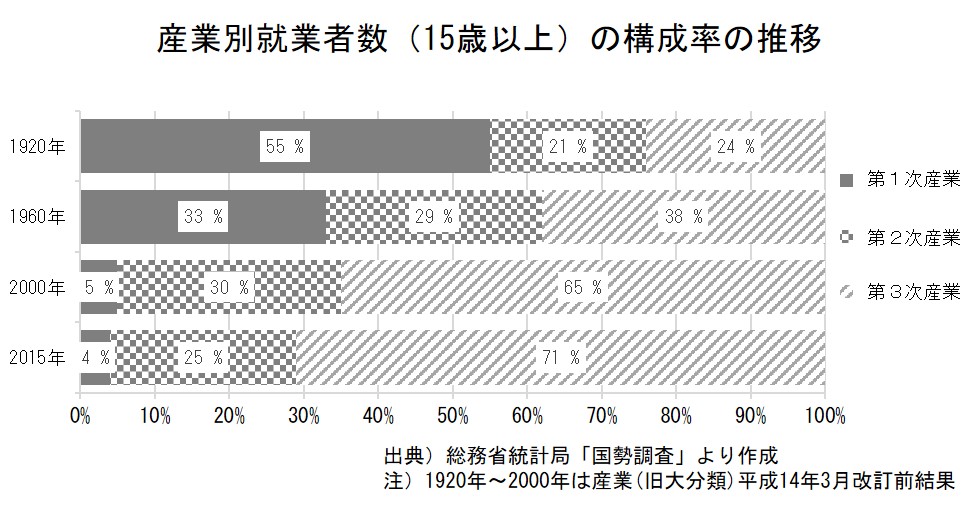
ここでは、仕事をしている人の数ではなく割合を知りたいので、棒の長さをそろえ、それぞれでの構成比をみてみました。1920年では第1次産業で働いている人が全体の半分以上であったのに、この割合は低下を続け、現在では4%程度であることがわかります。
-
どんなときに使うの?
帯グラフは、長さをそろえた棒を並べ、それぞれの棒の中に構成比を示すことによって、構成比の比較をするためのグラフです。
-
気をつけることは?
構成比をみることが目的なので、棒の長さは全て同じにします。
また、項目を並べる順番を途中で変えると、割合の変化がグラフを見てわからなくなってしまうので、一つのグラフの中では順番は変えないでおきます。
(上の例では、途中から第3次産業の就業者数が一番多くなっていますが、多い順に並べることはせずに、すべての年次にわたって第1次産業・第2次産業・第3次産業、の順に並べています)
-
やってみよう
総務省統計局「社会生活基本調査」では、1日の時間の使い方(睡眠、食事、学業、仕事、家事、趣味、等)を調べています。
年代別に、時間の使い方にどのような違いがあるか、帯グラフを描いて比べてみましょう。
ヒストグラム
-
たとえば・・・
クラスの中にも、背の高い人、低い人いろいろいます。どれくらいの身長の人が何人いるか、グラフで示してみましょう。
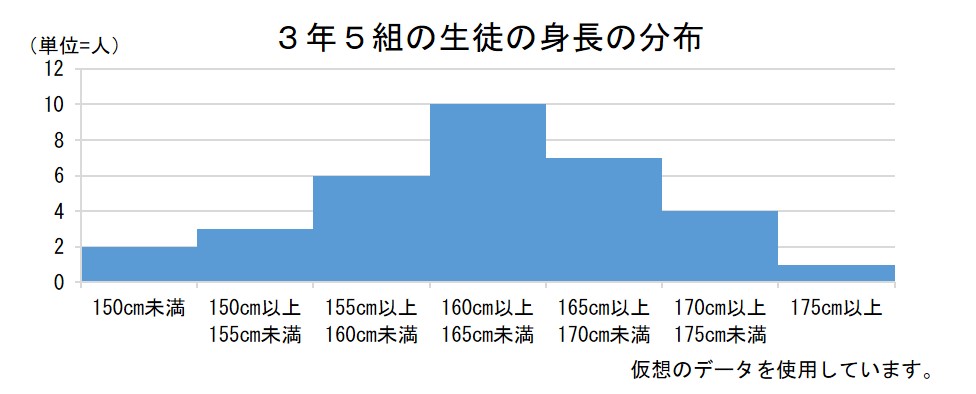
160cm以上165cm未満の人が一番多いことがわかりますね。
-
どんなときに使うの?
ヒストグラムは、データの散らばり具合をみるのに使われます。
横軸にデータの階級を、縦軸にその階級に含まれるデータの数(人数、個数など)をとって棒グラフで表します。 -
気をつけることは?
データの階級幅が異なるときには、棒グラフとは異なった扱いが必要です。
例えば、上記の例で、「165cm以上170cm未満と170cm以上175cm未満のところは人数も少ないから、まとめてしまおう」とした場合、「165cm以上175cm未満 7人」となりますが、それをそのままグラフに描くと、階級をまとめて人数が増えただけなのに、グラフの高さが高くなってしまって、誤解してしまうおそれがあります。そのため、そのような場合には、階級幅が2倍なので横幅を2倍にし、その代わりに高さを半分にして表示します(つまり、面積がデータの個数に比例するように描きます)。
また、グラフの両端(上の例では「150cm未満」と「175cm以上」)も、高さを隣よりも、(その階級の幅は5cmより長いので)低く表示します。
ヒストグラムを描く際には、「階級数をいくつに分ければよいか」というのが問題になります。通常は、5〜10くらいの階級数でヒストグラムを描いてみて、あまりデータの散らばりが見られなければ階級数を変えてみる、という方法をとります。
-
やってみよう
総務省統計局では、都道府県別や市町村別のデータをまとめてデータベースにしています。これを使って、「市町村別の中学校数の分布」などのヒストグラムを描いてみましょう。
「統計でみる都道府県・市区町村(社会・人口統計体系)」
レーダーチャート
-
たとえば・・・
みなさんの中には、「理科系には強いが、文科系がちょっとねぇ」とか、逆に「私は文科系の方が得意だ」という人もいるでしょう。そういったことを一目で示せないでしょうか。
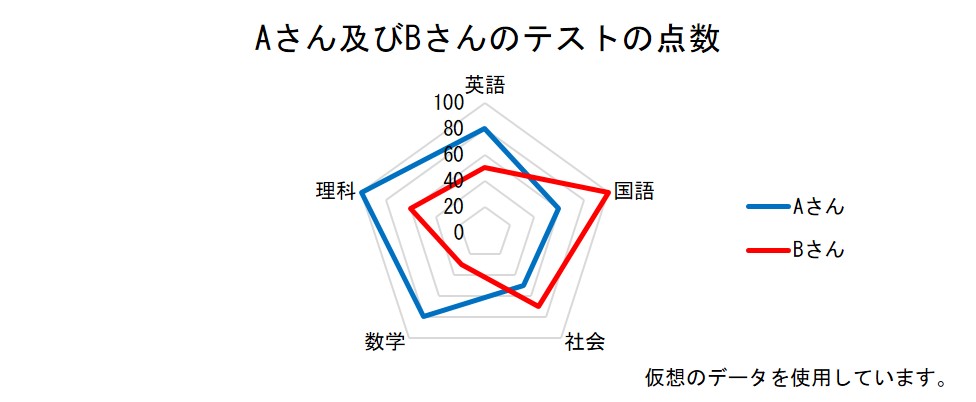
テストの成績をレーダーチャートで示すことにより、Aさんは理科や数学といった理科系は得意だが国語や社会といった文科系は苦手、Bさんは逆に文科系が強い、といったことがみてとれます。
-
どんなときに使うの?
レーダーチャートは、複数のデータ(指標)を一つのグラフに表示することにより、全体の傾向をつかむのに用いられるグラフです。
円を、データの項目数に応じて中心から放射状に線を引き、それぞれの線上に、データを表示します。そしてそれらを線で結んで、その形状を見ます。
-
気をつけることは?
レーダーチャートを描く際には、通常、「外に行くほど(データ値が大きいほど)良い」となるようにデータを選びます。
例えば、体力測定の結果をレーダーチャートに描く場合、幅跳びや反復横飛びは数字が大きいほど良いのですが、50m走などはタイムが短いほど良いので、単純に50m走のタイムでレーダーチャートを描くとおかしなグラフになってしまいます。そのような場合には、タイムではなくその逆数(つまり、「秒速○○m」とか)に直して、「データ値が大きいほど良い」データに変換する必要があります。
-
やってみよう
総務省統計局では、都道府県別や市町村別のデータをまとめてデータベースにしています。これを使って、皆さんの住んでいる都道府県・市町村の指標をレーダーチャートに描き、全国平均と比べてどうか、見てみましょう。
「統計でみる都道府県・市区町村(社会・人口統計体系)」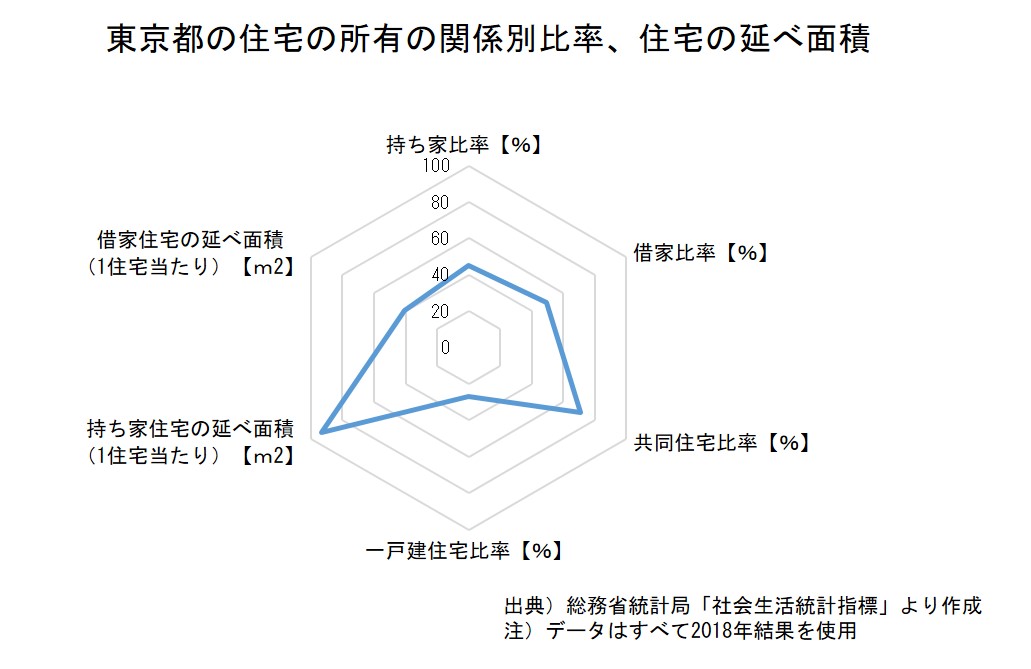
散布図
-
たとえば・・・
「数学が得意な人は理科も強い」とよく言われますが、本当にそうなのか、クラスの人の点数をグラフにしてみました。
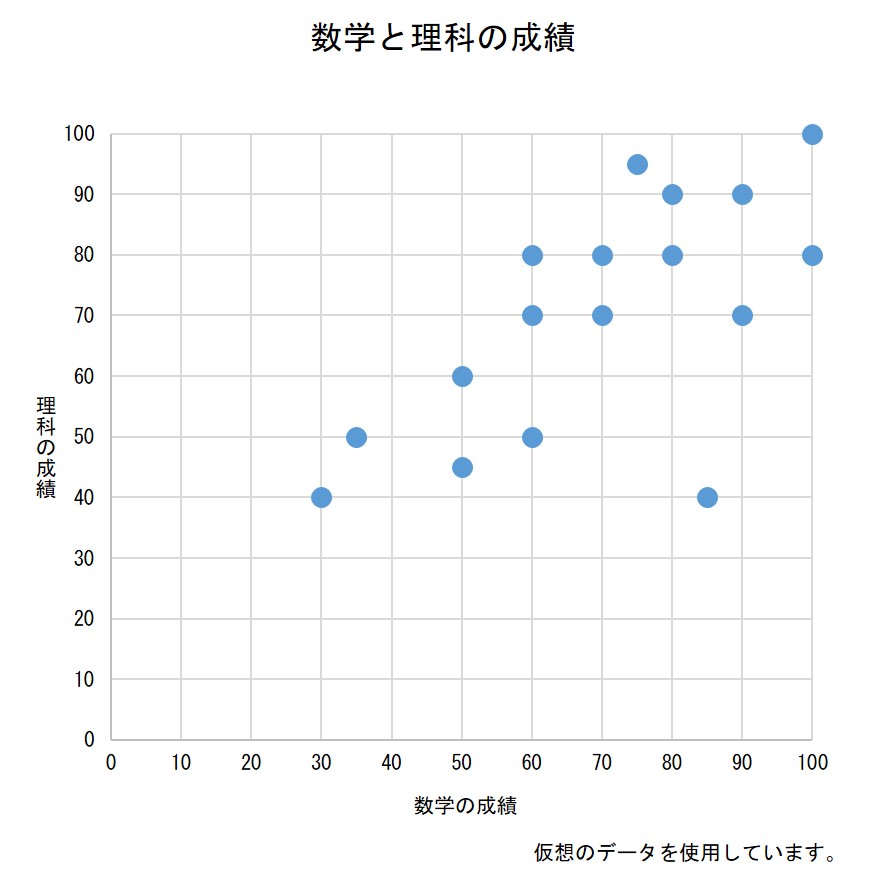
これをみると、確かに、数学の成績と理科の成績には関係がありそうに見えますね。
-
どんなときに使うの?
散布図は、縦軸と横軸にそれぞれ別の量をとり、データがあてはまるところに点を打って示す(「プロットする」といいます。)グラフです。2つの量に関係があるかどうかをみるのに使います。
-
気をつけることは?
散布図でわかることは、2つの量の間に関係があるかということだけであり、因果関係(どちらかが原因となって、もう一方が起こる)を示すものではありません。
例えば、働いている人について、血圧と給料の関係を散布図に描いたとします。普通は、年齢が高い人ほど血圧が高く、また年齢が高いほど給料も高くなるので、「血圧と給料には関係があります」という散布図になります。
でも、これから、「血圧を高くすると、給料が上がります」ということにはなりませんよね。 -
やってみよう
総務省統計局では、都道府県別や市町村別のデータをまとめてデータベースにしています。これを使って、県民所得や水道普及率、ごみの量などで、散布図を描いてみましょう。
「統計でみる都道府県・市区町村(社会・人口統計体系)」
箱ひげ図
-
たとえば・・・
お医者さんの数は、地域的に偏りがあると言われています。
都道府県別に見て、人口10万人当たり医師数(医療施設に従事する医師数)にどの程度ばらつきがあるか、グラフに表してみましょう。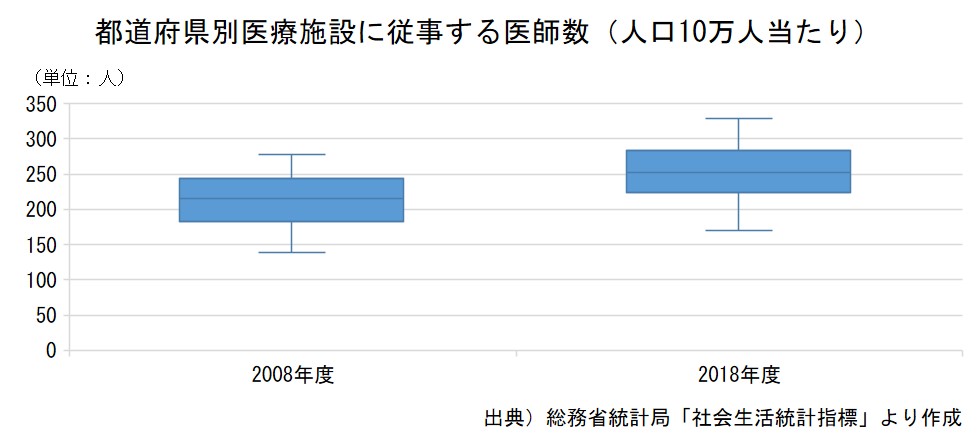
四角い箱の上下に、ひげが生えている形をしており、このようなグラフを「箱ひげ図」と呼びます。
この図では、ひげの一番下が最小値、箱の下部の辺が第1四分位数、真ん中の線が第2四分位数(中央値)、上部の辺が第3四分位数、そしてひげの一番上が最大値を表しています。
2008年度と2018年度とを比べると、全体として増加しているものの、最大値の増加が大きいことが見てとれます。
-
どんなときに使うの?
データのばらつき具合を比較するのに用います。1つのデータのばらつきを見るだけでしたらヒストグラムでも見られますが、ヒストグラムでは異なる複数のデータのばらつきを比較することは困難です。そのような場合、箱ひげ図により比較することができます。
-
気をつけることは?
ここで紹介したのは、ひげの両端がそれぞれ最小値、最大値になっている箱ひげ図ですが、中には、上下から10%点をひげの両端として描いている箱ひげ図もあります。
新聞やインターネットで箱ひげ図を見かけたときは、ひげの両端が何を表しているか、きちんと確認するとよいでしょう。
-
やってみよう
総務省統計局では、都道府県別や市町村別のデータをまとめてデータベースにしています。いろいろなデータを使って、箱ひげ図を描いてみましょう。
「統計でみる都道府県・市区町村(社会・人口統計体系)」
三角グラフ
-
たとえば・・・
日本でも、以前は農業のような第1次産業で働いている人が多かったのですが、工業化の進展により製造業などの第2次産業で働く人が増え、その後、サービス業などの第3次産業で働く人が増えてきました。
これを、国勢調査のデータで確認してみましょう。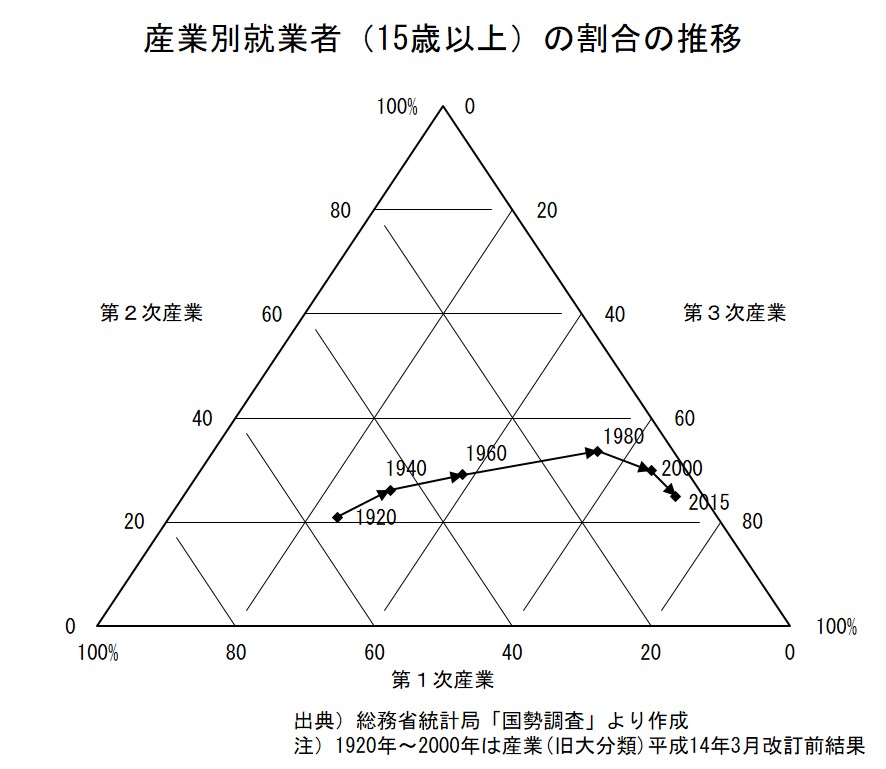
1920年 1940年 1960年 1980年 2000年 2020年 第1次産業 54.9% 44.6% 32.7% 10.9% 5.1% 4.0% 第2次産業 20.9% 26.2% 29.1% 33.6% 29.8% 25.0% 第3次産業 24.2% 29.2% 38.2% 55.4% 65.1% 71.0% 第1次産業の就業者の割合は、右上がりの斜線が目盛りになっています。1920年だと54.9%になっています。同様に、第2次産業の就業者の割合は底辺に平行な線が目盛り、第3次産業の就業者の割合は右下がりの斜線が目盛りです。
-
どんなときに使うの?
三角グラフは、3つの構成要素の比率を表すのに用いられます。社会科では上の例のような産業別の比率、理科では鉱物の組成比率を表すときなどに使われます。
なお、4以上の構成要素がある場合には三角グラフで表すことができません。(2次元の紙の上に書いているので、やむを得ないのですが・・。)その場合は、重要でない要素は「その他」にまとめてしまって、3つの構成要素にしてグラフを描きます。
-
気をつけることは?
ここで紹介したのは斜めの目盛線が入っている三角グラフですが、この他にも、辺からの距離でデータを表す三角グラフもあります。
例えば、底辺からの高さが、xの構成比を表す、ということになります。
自分が見ている三角グラフがどちらなのか、気をつけましょう。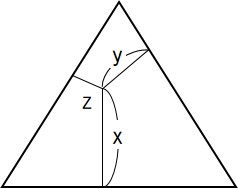
-
やってみよう
国勢調査には、都道府県別の、産業別就業者数のデータもあります。
あなたが住んでいる県でどうなっているか、隣の県はどうか、三角グラフに表してみましょう。
