どちらの扉を開けますか？

変えるべきか、変えないべきかそれが問題だ。まるで、ハムレットだね。

ぼうちゃんは車が欲しかったから、自分の判断を信じたいのよね。

どっちでも確率は同じよ。

ぼうちゃんのモンティ・ホール問題

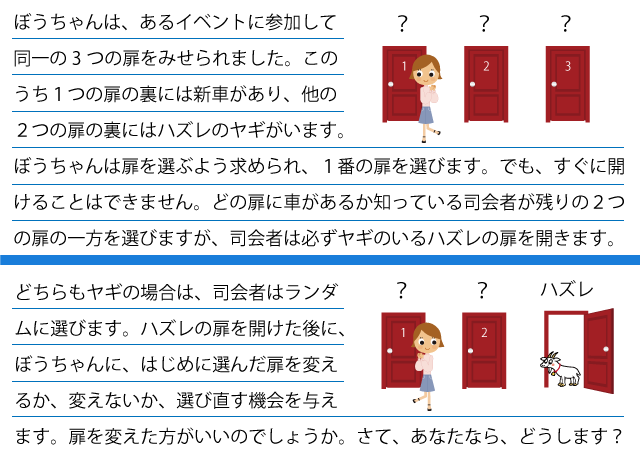
ぼうちゃんは、あるイベントに参加して同一の3つの扉をみせられました。このうち１つの扉の裏には新車があり、他の２つの扉の裏にはハズレのヤギがいます。ぼうちゃんは扉を選ぶよう求められ、１番の扉を選びます。でも、すぐに開けることはできません。どの扉に車があるか知っている司会者が残りの２つの扉の一方を選びますが、司会者は必ずヤギのいるハズレの扉を開きます。

?

どちらもヤギの場合は、司会者はランダムに選びます。ハズレの扉を開けた後に、ぼうちゃんに、はじめに選んだ扉を変えるか、変えないか、選び直す機会を与えます。扉を変えた方がいいのでしょうか。さて、あなたなら、どうします？

?

ハズレ

ぼうちゃんは、扉を変えずに、ハズレでした。みんなに扉を変えた方が確率は上がるといわれても、理由を聞く耳をもちません。

何で変えた方が当たる確率が高いわけ？ ２つの扉のどっちかでしょ。

確率は半々でしょ。運がなかったのよ。/p>

ぼうちゃん。ぼくらは確率論から計算した結果を答えているんだよ！

でも、結果論よね。変えて外れたらもっと悔しいワ！

ぼうちゃんは、２つの扉のどちらか１つが当たりだから、直感で、変えても変えなくても確率は同じだと思って、はじめに選んだ扉を変えなかったのよね。

そう

でもね、論理的に考えると、情報がないときと、ハズレの扉が開くという情報を得た後とでは確率に変化があるの。

ベイズの定理事前確率と事後確率ですね。

トーマス・ベイズ

ベイズの定理

トーマス・ベイズ(1702-1761）

イギリスの長老派の牧師・数学者であるトーマス・ベイズは、今から３世紀も前の人です。ベイズの定理の特殊な場合についての証明が死後発表されたことで知られます。ベイズの定理と組み合わせて確率的推論を行う方法がラプラスによって始められ、現在のベイズ統計学の端緒となりました。フィッシャーなどはベイズ統計を徹底的に否定しましたが、近年、急速に活用され始めています。

ベイズの定理　P(A|B) = P(B|A)P(A) / P(B)

たとえば、これってネットストアを例にすると、

P(A)＝女性が訪れる確率P(B)＝りんごが買われる確率P(B|A)＝女性の中でりんごを購入する確率P(A|B)＝りんごを購入した女性の確率と考える事ができるよね。これを「P(A)は原因を表すもの、P(B)は結果を表すもの」とすると、「りんごが買われたときに、女性の顧客だった」確率を計算するのにこの、ベイズの定理が役に立つ。

顧客

ネットストアの例みたいに、ベイズの定理で扱うものを「顧客と購買物」のような原因と結果の関係で考えると、 これって、購買物から顧客の性別を推測している事になるわけ。つまり、ベイズの定理は直接知る事ができない事を知るための理論（逆問題を解くための理論）とも言えるの。また、事前確率が事後確率を更新していると考えると、ベイズの定理の使い道がさらに広がるのよ。

ベイズの定理　事前確率P(A) と 事後確率P(B)

例えば、りんごを１回購入するよりも、２回購入する方が、りんごが好きな確率は高いと考えられる。この確率を計算する時、１回目に購入した時に計算した事後確率を２回目に購入した時の事後確率を計算する時の事前確率として使うんだ。こうした計算をベイズ更新と言い、ベイズ更新により、事前確率はどんどん修正されるので、事前確率には「たぶんこうだろう」という感じの主観的な確率（主観確率）を使うことができ、「自分が最初に思っていたものをデータで修正する」という使い方になる。

ベイズの定理の根底にあるのは、「観測された結果から見えない状態を推測し明らかにする」という考え方なんだ。

見えない状態を観測によって明らかにしていく

事前確率

ベイズの定理

観測１回目

事後確率

事前確率

ベイズの定理

観測２回目

事後確率

事前確率

ベイズの定理

観測３回目

事後確率

事前確率。

ベイズの定理

観測４回目

事後確率

確率はすべての合計が常に100％だから、わずかな可能性のモノも残して、無限に観測を行うことが可能なんだね。

ベイズの定理に基づき、観測された事実から、推定したい事柄を、確率的な意味で推論することをベイズ推定といい、ベイズ統計学の代表的な方法よ。でも、情報がないときには、とりあえず、「確率は全部等しい」と考える主観確率を積極的にとり入れているから、客観確率の立場の人からは科学的ではないと否定される概念でもあるのよ。でも、将来に対する「見込み、見通し、確信、信念、経験」 などを主観確率としてデータ解析にとり込むことで、さまざまな意思決定をサポートできるのよ。

モンティ・ホール問題は、ベイズの事後確率の例として、よく知られているの。

大さん、ぼうちゃんが気がついたわ。

あっ、そうか！扉の問題は事後確率だったんだ。

そう。やっと冷静になって、気がついたね。扉の問題もベイズの定理で計算してごらん。

ベイズの定理を使ったモンティ・ホール問題の証明

1番目の扉が当たりである確率をP(1car)、2番目の扉が当たりである確率を P(2car)、3番目の扉が当たりである確率を P(3car)とすると、はじめは、どの扉を選んでも車が当たる確率は理由不十分の原理で同じなので、P(1car) = P(2car) = P(3car) = 1/3となります。ここで、ぼうちゃんが１番目の扉を選んだとします。司会者が選べるのは２番目か3番目の車のない扉です。

あーあ、あのとき、冷静だったら、新車がもらえたのにね。

ここで、司会者が 3番目の扉を開けたとします。このとき、車があるのは 1 番目か2番目の扉の後ろで、比較する確率は、次の2つです。A) 3番目の扉が開いた後に　 1番目の扉の裏 に当たりの車がある確率B) 3番目の扉が開いた後に　 2番目の扉の裏 に当たりの車がある確率。

A) 1番目の扉の裏に当たりの車がある確率

P(1car)…1番目の扉に当たりの車がある確率 （事前確率）　P(3open)…3番目の扉が開く確率 P(3open | 1car)…1番目の扉に当たりの車があった場合、3番目の扉を開く確率（条件確率）P(1car | 3open)…3番目の扉が開いた後に1番目の扉に当たりの車がある確率

ハズレ

1番目の扉に当たりの車がある場合、司会者は2番目の扉と 3番目の扉のどちらも開けることができます。なので、P(3open|1car)は1/2です 。2番目の扉に当たりがある場合、司会者は3番目の扉しか開けることができないので、3番目の扉を開ける確率P(3open|2car)は100％で1/1 。また、3番目の扉に当たりの車がある場合、3番目の扉は開けられないのでP(3open|3car)は０。なので、P(3open) = P(3open|1car)P(1car) + P(3open|2car)P(2car) + P(3open|3car)P(3car) 　　　　 = 1/2 * 1/3 + 1 * 1/3 + 0 * 1/3 = 1 / 2以上をベイズの定理に当てはめると、P(1car|3open ＝ P(3open|1car) × P(1car) / P(3open)＝ （1/2） × （1/3） / （1/2） ＝ 1/3

3番目の扉が開いた後に1番目の扉に当たりの車がある確率1 /3。

B) 2番目の扉の裏に当たりの車がある確率

P(2car)…2番目の扉に当たりの車がある確率 （事前確率）　P(3open)…3番目の扉が開く確率 P(3open | 2car)…2番目の扉に当たりの車があった場合、3番目の扉を開く確率（条件確率）P(2car | 3open)…3番目の扉が開いた後に２番目の扉に当たりの車がある確率

ハズレ

★

P(3open) はA)の場合と同じで 1 / 2。P(2car) は、1/3、P(3open|2car)は2番目の扉に当たりがある場合は、司会者は、３番目の扉しか開けることが出来ないので、A)と同じ、1/1。結果、P(2car|3open) ＝ P(3open|2car) × P(2car) / P(3open)＝ （1/1） × （1/3） / （1/2） ＝ 2/3

3番目の扉が開いた後に2番目の扉に当たりの車がある確率2 /3。

みんな、ありがとう。扉を変えると当たる確率は２倍になるのね。

ところで、ぼうちゃん、もらったヤギは、どうするんですか？

ピアソンカフェで預かってもらってチーズを作って売るの。

メス？

オス